Question

How many cubical wood pieces with length 25cm can be prepared by a cubical beam with length 2 m?

Answer 1

Hint: We have to find the number of cubical woods with length 25cm which can be prepared from a cubical beam of length 2m. As all the smaller cubical blocks are carved out from the bigger cubical beam of length 2m, so the total volume of all small cubical blocks will be equal to the volume of the bigger cubical beam which has length 2m. Assume, the number of smaller cubical blocks is x. Then solve it further and find the value of x.

Complete step-by-step answer:

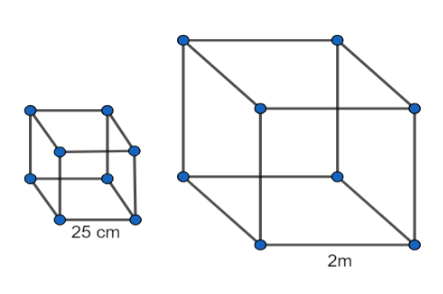
Let the number of smaller cubical wood pieces with length 25cm that can be prepared by a cubical beam with length 2 m be x.
Volume of one smaller cubical wood piece = \[{{(25)}^{3}}c{{m}^{3}}\] .
Volume of all smaller cubical wood pieces = \[x{{(25)}^{3}}c{{m}^{3}}\] …………..(1)
We know that, 1m=100cm.
According to the question, we have the length of the bigger cubical beam = 2m=2(100)cm=200cm.
Volume of the bigger cubical beam = \[{{(200)}^{3}}c{{m}^{3}}\] …………………..(2)
As all the smaller cubical blocks are carved out from the bigger cubical beam of length 2m, so total volume of all smaller cubical blocks will be equal to the volume of the bigger cubical beam which has length 2m.
Volume of all smaller cubical wood pieces = Volume of the bigger cubical beam
\[\begin{align}
  & \Rightarrow x{{(25)}^{3}}c{{m}^{3}}={{(200)}^{3}}c{{m}^{3}} \\
 & \Rightarrow x=\dfrac{{{(200)}^{3}}}{{{(25)}^{3}}} \\
 & \Rightarrow x={{8}^{3}}=512 \\
\end{align}\]
Hence, the number of cubical wood pieces with length 25cm that can be prepared by the cubical beam with length 2 m is 512.

Note: In this question, one can write the volume of the bigger cubical beam as \[{{2}^{3}}{{m}^{3}}\] and then solve.
The volume of all smaller cubical wood pieces = Volume of the bigger cubical beam
One must be extra sure about the unit conversions and should be aware that all the units are the same on both sides of the equations.