Question

Construct a\[\Delta ABC\]in which base BC = 6 cm, AB = 5.5 cm and\[\angle ABC={{120}^{\circ }}\].
(i) Construct a circle circumscribing the\[\Delta ABC\]
(ii) Draw a cyclic quadrilateral ABCD so that D is equidistant from B and C.

Answer 1

Hint:- Draw the bare BC = 6 cm. Construct \[{{120}^{\circ }}\] from point B and take AB = 5.5 cm. Join AC to get \[\Delta ABC\]. Bisect sides AB and BC to get the center of the circle O.

Complete step-by-step solution -
Taking radius OA, draw the circle, angle bisector of \[\angle ABC\] bisector of BC will meet at point D. Join CD and AD. You will get the cyclic quadrilateral ABCD.
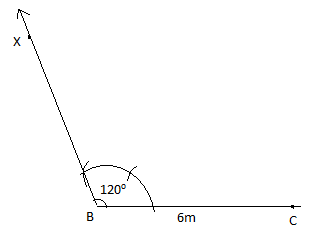
First let us draw a line segment BC of length 6 cm. At B, draw a ray BX making an angle of \[{{120}^{\circ }}\] with BC.
Now, we have to mark angle \[{{120}^{\circ }}\] on ray BX. Using the compass put the pin at B and C. Cut an arc over BC. From the arc point on line BC make a cut of the same length on the arc. It forms \[{{60}^{\circ }}\]. From the \[{{60}^{\circ }}\] cut makes another cut of the same length in the arc that makes \[{{120}^{\circ }}\].

With B as center and radius 5.5 cm, draw an arc to cut the ray BX at A. Join AC and we will get \[\Delta ABC\]. Then draw the perpendicular bisector of AB and BC to meet at point O.

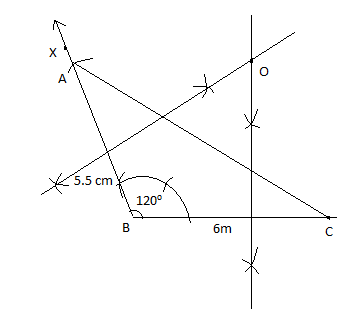
To draw the perpendicular bisector, take more than half of the length of BC. Cut an arc from B and C, above and below the line. Join the cut it gives the perpendicular bisector of BC. Similarly, draw the perpendicular bisector of AB. Their bisector intersects at point O.

Now with O as the center of the circle and radius as OA, draw a circle. The circle will circumscribe \[\angle ABC\]. Then draw the angle bisector of \[\angle ABC\].
The angle bisector of \[\angle ABC\] and the perpendicular bisector of the line segment BC will intersect at point D. This point D will be equidistant from points B and C.
Then join AD and DC to obtain the required cyclic quadrilateral ABCD.
(i) Construct the circle circumscribing triangle ABC.
Hence we got the circle circumscribing \[\Delta ABC\].

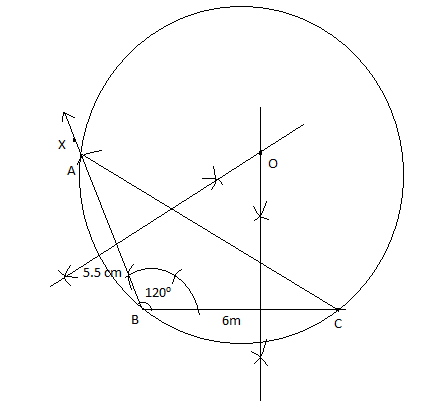
(ii) Cyclic quadrilateral ABCD is thus drawn where D is equidistant from B and C. Bisector of angle \[{{120}^{\circ }}\] and mid segment of BC meets at point D. Joining CD, BD and CD is equidistant from D. We get cyclic quadrilateral ABCD.

Note:- In questions like these it’s important to know the basic constructions like \[{{45}^{\circ }},{{60}^{\circ }},{{90}^{\circ }},{{120}^{\circ }}\] etc. In this question we constructed \[{{60}^{\circ }},{{90}^{\circ }},{{120}^{\circ }}\]. By knowing the basic constructions like these we could easily draw cyclic quadrilateral ABCD.