Question

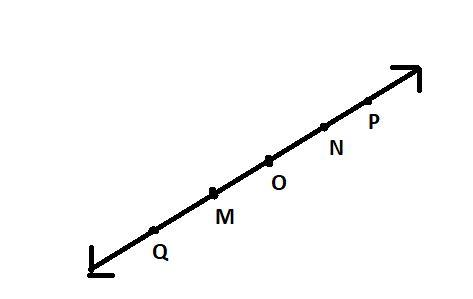
Consider the following figure of line$\overline {MN} $. Say whether following statement is true or false in context of the given figure
Ray $\overrightarrow {OP} $is different from ray$\overrightarrow {QP} $.
$A.$True
$B.$False

Answer 1

Hint: - Here we use the property of line and ray to solve the question.

When we read the statement we observe that both rays have different starting points. We know that two rays are called the same if they have the same direction and same end point or starting point.
Here, ray$\overrightarrow {OP} $and $\overrightarrow {QP} $ have same direction but different initial point so they are different
Hence we can say that the given statement is a false statement.
So option B is the correct answer.

Note:- Whenever we face such a type of question we have to go through its diagram and apply the property of that figure to verify the answers.