Question

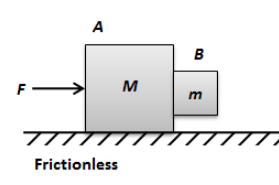
Coefficient of friction between A and B is \[\mu \]. The minimum force F with which A will be pushed such that B will not slip down is:

A. \[\dfrac{{Mg}}{\mu }\]
B. \[\dfrac{{mg}}{\mu }\]
C. \[\dfrac{{\left( {M + m} \right)g}}{\mu }\]
D. \[\dfrac{{\left( {M - m} \right)g}}{\mu }\]

Answer 1

Hint: Express the applied force F using Newton’s second law. Determine the normal force due to the block A on the block B. The block B will not slip down if the weight of the block B is balanced by the friction between the two blocks.

Formula used:
Frictional force, \[f = \mu N\],
where, \[\mu \] is the coefficient of friction and N is the normal force.

Complete step by step answer:
Let us express the applied force on the system of two blocks A and B using Newton’s second law of motion as follows,
\[F = \left( {M + m} \right)a\] …… (1)
Here, \[a\] is the acceleration produced in the two blocks.

We can see the applied force F on the block A exert a force on the block B which is the normal force. The direction of this normal force is the same as the direction of the applied force. Let us express the normal force acting on the block B as,
\[N = ma\] …… (2)

Now, for block B to not slip down, the static friction between the two blocks must be equal to the weight of the block B.

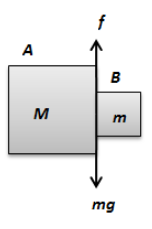
From the above free body diagram, we can write,
\[{f_s} = mg\]
\[ \Rightarrow \mu N = mg\]
Using equation (2) in the above equation, we get,
\[\mu ma = mg\]
\[ \Rightarrow a = \dfrac{g}{\mu }\]
Substituting the above equation in equation (1), we get,
\[F = \left( {M + m} \right)\left( {\dfrac{g}{\mu }} \right)\]
\[ \therefore F = \dfrac{{\left( {M + m} \right)g}}{\mu }\]

So, the correct answer is option C.

Note:We have expressed the normal force as \[N = ma\] because it is the force acting on block B and the acceleration of block B is the same as the acceleration of the system of two blocks. We can apply Newton’s second law only in a single direction. The acceleration produced by the applied force is in the horizontal direction and in the vertical direction, the acceleration is due to the acceleration due to gravity.