Question

Classify the angles whose magnitudes are given below:
$91^\circ $

Answer 1

Hint: When two rays intersect each other and form an angle between $0^\circ $ to $90^\circ $, we can say that the angle between them is acute.
When two rays intersect each other and the angle between them is $90^\circ $, we can say that the angle between them is the right angle.
When two rays intersect each other and the angle between them is more than $90^\circ $ and less than $180^\circ $, then the angle is said to be an obtuse angle.

Complete step-by-step solution:
In this question, we are given a measure of an angle and we need to find out which type of angle it is.
Now, angles are the base of geometry and there are 4 types of angles in geometry.
Acute Angle:
When two rays intersect each other and form an angle between $0^\circ $ to $90^\circ $, we can say that the angle between them is acute.
For example: $30^\circ ,45^\circ ,60^\circ $

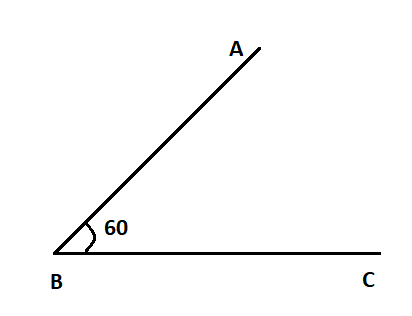
Right angle:
When two rays intersect each other and the angle between them is $90^\circ $, we can say that the angle between them is the right angle.

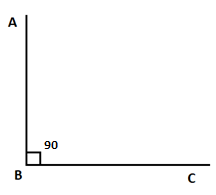
Obtuse angles:
When two rays intersect each other and the angle between them is more than $90^\circ $ and less than $180^\circ $, then the angle is said to be obtuse angle.
For example: $95^\circ ,120^\circ ,130^\circ ,150^\circ $

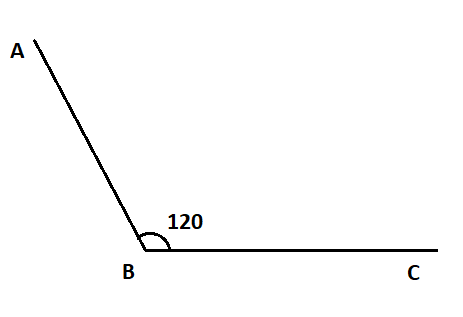
Straight angle:
When the angle between two rays is equal to $180^\circ $, then we can say that the angle is straight angle.
For example:

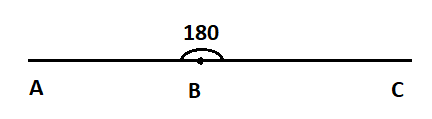
Now, in our question, we are given an angle with measure $91^\circ $ which is greater than $90^\circ $ and less than $180^\circ $. Therefore, the given angle is obtuse angle.

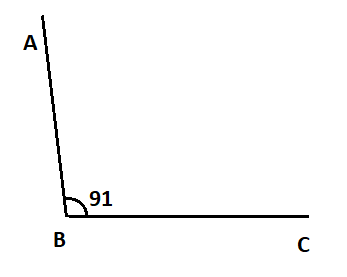
Note: FOr answering this type of question we should have a theoretical concept of angles.
> When the sum measure of two angles equals to $90^\circ $, then the two angles are said to be complementary angles.
> When the sum measure of two angles equals to $180^\circ $, then the two angles are said to be supplementary angles.