Question

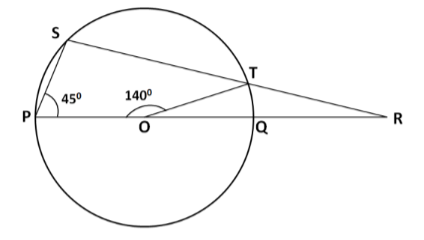
Centre of circle as shown in figure. Find $\angle RQT$ and $\angle RTQ$

Answer 1

Hint: First we need to complete the triangle RTQ since the angles $\angle RQT$ and $\angle RTQ$ belong to it. Then, applying the cyclic quadrilateral property on the quadrilateral PQTS, which states that the sum of the opposite angles is equal to ${{180}^{\circ }}$, we can determine the angle $\angle TOS$. Then, using the linear pair property and the angle sum property, we can determine the remaining angles including the angles $\angle RQT$ and $\angle RTQ$ which are asked in the question.

Complete step by step solution:
Since we have to determine the values of the angles $\angle RQT$ and $\angle RTQ$ which lie inside the triangle RTQ, we join the points T and Q to complete the triangle RTQ as shown in the below figure.

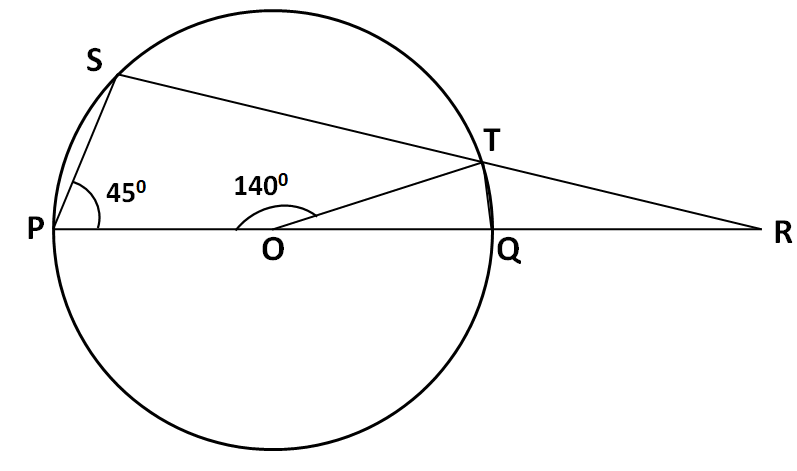
Now, since all the points P, Q, T, and S lie on the circumference of the circle, so the quadrilateral PQTS formed by these points is a cyclic quadrilateral. We know that the sum of the opposite angles in a cyclic quadrilateral is equal to ${{180}^{\circ }}$. So we can write
$\Rightarrow \angle P+\angle QTS={{180}^{\circ }}$
From the above figure, we have $\angle P={{45}^{\circ }}$. Substituting this in the above equation, we get
\[\begin{align}
  & \Rightarrow {{45}^{\circ }}+\angle QTS={{180}^{\circ }} \\
 & \Rightarrow \angle QTS={{180}^{\circ }}-{{45}^{\circ }} \\
 & \Rightarrow \angle QTS={{135}^{\circ }}........(i) \\
\end{align}\]
Now, from the figure above, we can see that the angles \[\angle QTS\] and \[\angle RTQ\] are forming a linear pair. We know that the sum of the angles in a linear pair is equal to ${{180}^{\circ }}$. So we can write
$\Rightarrow \angle QTS+\angle RTQ={{180}^{\circ }}$
Substituting (i) in the above equation, we get
\[\begin{align}
  & \Rightarrow {{135}^{\circ }}+\angle RTQ={{180}^{\circ }} \\
 & \Rightarrow \angle RTQ={{180}^{\circ }}-{{135}^{\circ }} \\
 & \Rightarrow \angle RTQ={{45}^{\circ }}........(ii) \\
\end{align}\]
Now, from the above figure we can see that the angles \[\angle POT\] and \[\angle TOQ\] are also forming a linear pair. So we have
$\Rightarrow \angle POT+\angle TOQ={{180}^{\circ }}$
From the figure, $\angle POT={{140}^{\circ }}$. Substituting this in the above equation we get
\[\begin{align}
  & \Rightarrow {{140}^{\circ }}+\angle TOQ={{180}^{\circ }} \\
 & \Rightarrow \angle TOQ={{180}^{\circ }}-{{140}^{\circ }} \\
 & \Rightarrow \angle TOQ={{40}^{\circ }}.........(iii) \\
\end{align}\]
Now, we know that the distances of the centre from each point on a circle are equal. So we can write
$\Rightarrow OT=OQ$
We know that the angles opposite to the equal sides are equal. Therefore from the triangle OTQ we have
\[\Rightarrow \angle OQT=\angle OTQ........(iv)\]
From angle sum property in the triangle OTQ we have
\[\angle OQT+\angle OTQ+ \angle TOQ={{180}^{\circ }}\]
Putting (ii) and (iv) we get
\[\begin{align}
  & \Rightarrow \angle OTQ+\angle OTQ+\angle TOQ={{180}^{\circ }} \\
 & \Rightarrow 2\angle OTQ+{{40}^{\circ }}={{180}^{\circ }} \\
 & \Rightarrow 2\angle OTQ={{180}^{\circ }}-{{40}^{\circ }} \\
 & \Rightarrow 2\angle OTQ={{140}^{\circ }} \\
 & \Rightarrow \angle OTQ={{70}^{\circ }}........(v) \\
\end{align}\]
Since \[\angle OTQ\] and \[\angle RTQ\] form a linear pair, we have
\[\Rightarrow \angle RTQ+\angle QTQ={{180}^{\circ }}\]
Putting (v) we get
\[\begin{align}
  & \Rightarrow \angle RTQ+{{70}^{\circ }}={{180}^{\circ }} \\
 & \Rightarrow \angle RTQ={{180}^{\circ }}-{{70}^{\circ }} \\
 & \Rightarrow \angle RTQ={{110}^{\circ }} \\
\end{align}\]
Hence, the angles $\angle RQT$ and $\angle RTQ$ are respectively equal to \[{{110}^{\circ }}\] and \[{{45}^{\circ }}\].

Note: We can also use the relation between the angle subtended by a chord on the centre of the circle and that subtended at some point on the circumference to solve this question. Also, the angle sum property may be applied in any of the triangles in the given figure. So there are many methods to solve this question and you can solve any of them.