Question

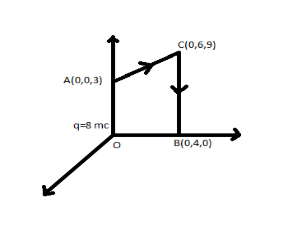
Calculate the work done in taking a charge $ - 2 \times {10^{ - 9}}C$ from A and B via C (in diagram).
          

A. 0.2 J
B. 1.2 J
C. 2.2 J
D. Zero

Answer 1

Hint:To calculate the work done in moving the charge from point A to point B firstly, calculate the potential at the point A and B respectively. Then, calculate the potential difference between the point A and B created due to charge present at the origin. At last multiply the calculated potential difference with the charge moving from point A and B.

Formula used: $W = {q_1}\left( {{V_B} - {V_A}} \right)$
Here, $q_1$ is the charge which moves. ${V_B}$ is the potential at B due to q and ${V_A}$ is the potential at A due to q.

Complete step by step answer:
In this question, we want to find out the work done in bringing a charge $ - 2 \times {10^{ - 9}}C$ from A to B via C. But as we know that moving a charge in electric field is independent of path chosen to move the charge in electric field and depends only on electric potential difference between them.
          

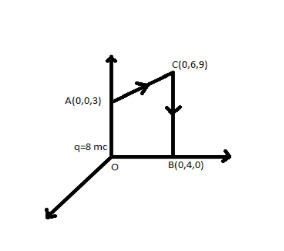
If charge directly moves from A to B then the result will be the same.
          

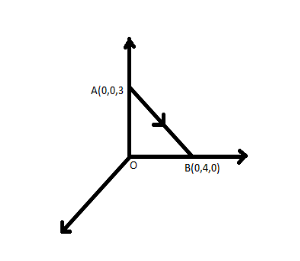
The only thing we need to do is to find the potential at A due to charge \[q = 8mc\] at the origin i.e., .
 ${r_{OA}} = $ Distance between origin and the point \[A = 3cm\].
Similarly, potential at B due to charge, \[q = 8mc\]at the origin

${r_{OB}} = $ Distance between origin and the point \[B = 4cm\].
$\therefore work\;done = {q_1}\left( {{V_B} - {V_A}} \right)$
Now, by substituting the values we get,

Now, putting all the values,
${q_1} = - 2 \times {10^{ - 9}}C$
$q = 8mc = 8 \times {10^{ - 3}}C$

${r_{OB}} = 4cm$
${r_{OA}} = 3cm$
$W = - 2 \times {10^{ - 9}} \times 8 \times {10^{ - 3}} \times 9 \times {10^9}\left( {\dfrac{1}{4} - \dfrac{1}{3}} \right)$
\[\;\therefore W = 1.27{\text{ }}J\;\] (Answer)

Note:Charge which is moving from one point to another is always multiplied to potential difference between the points, whatever the path of charge will be.