Question

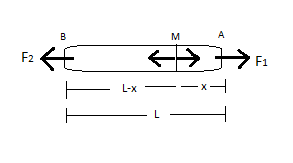
Calculate the tension T in the rope at distances x from end A in the following diagram, assuming that F1>F2.

Answer 1

Hint: In this question, we need to determine the tension in the rope at a point which is ‘x’ distance from the end A. For this, we will draw the free body diagram of the rope and by using Newton's second law of motion.

Complete step by step answer:
Given that the force F1>F2.
We know by the newton’s second law of motion
\[F = ma - - (i)\]
Here as two forces are acting where F1>F2, so we can write equation (i) as
\[{F_1} - {F_2} = ma\]
This can be written as
\[a = \dfrac{{{F_1} - {F_2}}}{m} - - (ii)\]
Now, since we have to find the tension T in rope from end A so we will draw the free body diagram for the side A at distance x

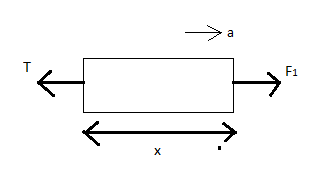
We know that whenever a tensile force is acting on any object, a tension is experienced in the direction opposite to the force
From the above free body diagram, we can write
\[{F_1} - T = ma - - (iii)\]
Here mass m is the linear mass density, which is equal to
\[m = \dfrac{{Mx}}{L}\]
Now by substituting linear mass density in equation (iii), we get
\[{F_1} - T = \dfrac{{Mx}}{L} \times a\]
Now substitute the value of acceleration from equation (ii), we further get
\[
  {F_1} - T = \dfrac{{mx}}{L} \times \dfrac{{{F_1} - {F_2}}}{m} \\
  {F_1} - T = \dfrac{x}{L} \times \left( {{F_1} - {F_2}} \right) \\
  {F_1} - \dfrac{x}{L} \times \left( {{F_1} - {F_2}} \right) = T \\
  {F_1} - \dfrac{{{F_1}x}}{L} + \dfrac{{{F_2}x}}{L} = T \\
  {F_1} + \dfrac{x}{L} \times \left( {{F_2} - {F_1}} \right) = T \\
 \]

Hence the tension T in the rope at distances x from end A
\[T = {F_1} + \dfrac{x}{L} \times \left( {{F_2} - {F_1}} \right)\]

Note: It is worth noting down here that if the tension exerted on the rope is more than the tensile strength of the rope, then the rope will break; otherwise, not. Moreover, as the pull force on the rope at the side A of the rope is more than the side B so, the acceleration will be towards A only.