
Calculate the resonance energy of \[{{N}_{2}}O\] from the following data:
\[\Delta {{H}_{f}}^{\circ }\,\]of \[{{N}_{2}}O\] = \[134KJ\,mo{{l}^{-1}}\]
Bond energy of \[N-O\], \[N=O\], \[N\equiv N\] and \[O=O\] bonds are 222, 607, 946 and
498 \[kJ\,mo{{l}^{-1}}\] respectively.
Answer
595.5k+ views
Hint: Many compounds exhibit resonance. Due to resonance they exist in a structure which is different from the expected one and more stable. Resonance energy can be calculated by the formula:
Resonance energy = \[\Delta {{H}_{f}}^{\circ }(actual)-\Delta {{H}_{f}}^{\circ }(calculated)\]
Complete step by step solution:
Before we start solving let us define some basic terms:
The standard enthalpy change of formation (\[\Delta {{H}_{f}}^{\circ }\,\]) of a compound is defined as the heat change which takes place when one mole of the compound is formed from its elements under standard conditions, usually at 25℃ and 1 atm.
For example:
For 1 mole of water
\[{{H}_{2}}+\dfrac{1}{2}{{O}_{2}}\to {{H}_{2}}O\,\,\,\,\,\,\,\,\,\,\Delta H_{f}^{\circ }=-286\,kJ\,mo{{l}^{-1}}\]
The standard enthalpy change of a reaction (\[\Delta H_{r}^{\circ }\]) is defined as the heat change which takes place when equation quantities of materials react under standard conditions, usually at 25℃ and 1 atm, and with everything in its standard state.
For example:
\[2{{H}_{2}}+{{O}_{2}}\to 2{{H}_{2}}O\,\,\,\,\,\,\,\,\,\,\Delta H_{r}^{\circ }=-572\,kJ\,mo{{l}^{-1}}\]
It is mathematically given as:
\[\Delta H_{r}^{\circ }\text{=}\sum{\text{Bond enthalpy of}\,\text{product-}\sum{\text{Bond enthalpy}\,\text{of}\,\text{reactants}}}\]
We have been provided in the question that the:
\[\Delta {{H}_{f}}^{\circ }\,\]of \[{{N}_{2}}O\] = \[134KJ\,mo{{l}^{-1}}\]
Bond energy of \[N-O\]= 222 \[kJ\,mo{{l}^{-1}}\]
Bond energy of \[N=O\]= 607 \[kJ\,mo{{l}^{-1}}\]
Bond energy of \[N\equiv N\]= 946 \[kJ\,mo{{l}^{-1}}\]
Bond energy of \[O=O\]= 498 \[kJ\,mo{{l}^{-1}}\]
The chemical reaction for the formation of one mole of \[{{N}_{2}}O\] will be,
\[N\equiv N+\dfrac{1}{2}(O=O)\to N=N=O\]
We know that in a reaction,
\[\Delta H_{r}^{\circ }\text{=}\sum{\text{Bond enthalpy of}\,\text{product-}\sum{\text{Bond enthalpy}\,\text{of}\,\text{reactants}}}\]
\[\Delta H_{f({{N}_{2}}O)}^{\circ }=\left[ \Delta {{H}_{(N\equiv N)}}+\dfrac{1}{2}\Delta {{H}_{(O=O)}} \right]-\left[ \Delta {{H}_{(N=N)}}+\Delta {{H}_{(N=O)}} \right]\]
Putting the values in the above equation,
\[\begin{align}
& \Delta H_{f({{N}_{2}}O)}^{\circ }=\left[ 946+\dfrac{1}{2}\times (498) \right]-\left[ 607+418 \right] \\
& \,\,\,\,\,=\,1195-1025 \\
& \,\,\,\,\,=\,170\,kJ\,mo{{l}^{-1}} \\
\end{align}\]
So, the calculated heat of formation is \[170\,kJ\,mo{{l}^{-1}}\].
Using formula provided in the hint,
Resonance energy = \[\Delta {{H}_{f}}^{\circ }(actual)-\Delta {{H}_{f}}^{\circ }(calculated)\]
= 82-170
= -88 \[kJ\,mo{{l}^{-1}}\]
Therefore, the resonance energy is calculated as -88 \[kJ\,mo{{l}^{-1}}\].
Note: In the case of Nitrous oxide, the electronegativity of oxygen is higher than nitrogen, meaning a negative charge on oxygen atom will be more stable than a negative charge on nitrogen atom. Stability order: II>I>III
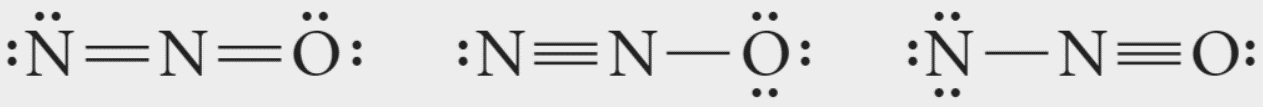
Resonance energy = \[\Delta {{H}_{f}}^{\circ }(actual)-\Delta {{H}_{f}}^{\circ }(calculated)\]
Complete step by step solution:
Before we start solving let us define some basic terms:
The standard enthalpy change of formation (\[\Delta {{H}_{f}}^{\circ }\,\]) of a compound is defined as the heat change which takes place when one mole of the compound is formed from its elements under standard conditions, usually at 25℃ and 1 atm.
For example:
For 1 mole of water
\[{{H}_{2}}+\dfrac{1}{2}{{O}_{2}}\to {{H}_{2}}O\,\,\,\,\,\,\,\,\,\,\Delta H_{f}^{\circ }=-286\,kJ\,mo{{l}^{-1}}\]
The standard enthalpy change of a reaction (\[\Delta H_{r}^{\circ }\]) is defined as the heat change which takes place when equation quantities of materials react under standard conditions, usually at 25℃ and 1 atm, and with everything in its standard state.
For example:
\[2{{H}_{2}}+{{O}_{2}}\to 2{{H}_{2}}O\,\,\,\,\,\,\,\,\,\,\Delta H_{r}^{\circ }=-572\,kJ\,mo{{l}^{-1}}\]
It is mathematically given as:
\[\Delta H_{r}^{\circ }\text{=}\sum{\text{Bond enthalpy of}\,\text{product-}\sum{\text{Bond enthalpy}\,\text{of}\,\text{reactants}}}\]
We have been provided in the question that the:
\[\Delta {{H}_{f}}^{\circ }\,\]of \[{{N}_{2}}O\] = \[134KJ\,mo{{l}^{-1}}\]
Bond energy of \[N-O\]= 222 \[kJ\,mo{{l}^{-1}}\]
Bond energy of \[N=O\]= 607 \[kJ\,mo{{l}^{-1}}\]
Bond energy of \[N\equiv N\]= 946 \[kJ\,mo{{l}^{-1}}\]
Bond energy of \[O=O\]= 498 \[kJ\,mo{{l}^{-1}}\]
The chemical reaction for the formation of one mole of \[{{N}_{2}}O\] will be,
\[N\equiv N+\dfrac{1}{2}(O=O)\to N=N=O\]
We know that in a reaction,
\[\Delta H_{r}^{\circ }\text{=}\sum{\text{Bond enthalpy of}\,\text{product-}\sum{\text{Bond enthalpy}\,\text{of}\,\text{reactants}}}\]
\[\Delta H_{f({{N}_{2}}O)}^{\circ }=\left[ \Delta {{H}_{(N\equiv N)}}+\dfrac{1}{2}\Delta {{H}_{(O=O)}} \right]-\left[ \Delta {{H}_{(N=N)}}+\Delta {{H}_{(N=O)}} \right]\]
Putting the values in the above equation,
\[\begin{align}
& \Delta H_{f({{N}_{2}}O)}^{\circ }=\left[ 946+\dfrac{1}{2}\times (498) \right]-\left[ 607+418 \right] \\
& \,\,\,\,\,=\,1195-1025 \\
& \,\,\,\,\,=\,170\,kJ\,mo{{l}^{-1}} \\
\end{align}\]
So, the calculated heat of formation is \[170\,kJ\,mo{{l}^{-1}}\].
Using formula provided in the hint,
Resonance energy = \[\Delta {{H}_{f}}^{\circ }(actual)-\Delta {{H}_{f}}^{\circ }(calculated)\]
= 82-170
= -88 \[kJ\,mo{{l}^{-1}}\]
Therefore, the resonance energy is calculated as -88 \[kJ\,mo{{l}^{-1}}\].
Note: In the case of Nitrous oxide, the electronegativity of oxygen is higher than nitrogen, meaning a negative charge on oxygen atom will be more stable than a negative charge on nitrogen atom. Stability order: II>I>III
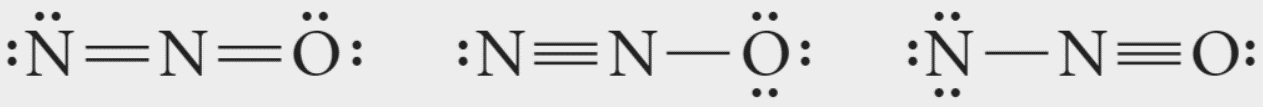
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




