Question

How do you calculate the mass of the sun,\[{M_{Sun}}\], using Kepler’s third law (\[{T^2} = \dfrac{{4{\pi ^2}{r^3}}}{{G{M_{sun}}}}\])?

Answer 1

Hint: Kepler discovered three empirical laws that accurately described the motion of the planets. The three laws may be states as,
(I) Planets move in an elliptical orbit, with the sun at one focus of the ellipse. This law is also known as the law of elliptical orbits and obviously gives the shape of the orbits of the planets around the sun.
(ii) The radius vector which is drawn from the sun to a planet, sweeps out equal areas in equal intervals of time, i.e. its areal velocity (or the area swept out by it per unit time) will remain constant. This law is also known as the law of areas and gives the relationship between the orbital speed of the planet and its distance from the sun.
(iii) The square of the time taken in one revolution of a planet is proportional to the cube of the semi-major axis of its orbit. This law is also known as the law of time period and gives the relationship between the size of the orbit of a planet and the time period of revolution.

Complete step by step answer:
To calculate the required expression for Kepler’s third law for planetary motion:
i.e. \[{T^2} = \dfrac{{4{\pi ^2}{r^3}}}{{G{M_{sun}}}}\], we will assume that the path of the planets are elliptical with centre of earth at a focus. However the difference in the major and minor axes is so small that they can be treated as nearly circular to avoid the sophisticated calculations.
The necessary condition that planets revolve around the sun is that- the centripetal force to the planet is being provided by the gravitational force exerted by the earth on the planet.

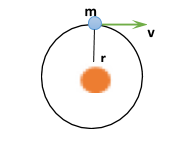
Thus,
\[\dfrac{{G{M_{sun}}m}}{{{r^2}}} = \dfrac{{m{v^2}}}{r}\]……………….. (i)
Where,
-m is the mass of the planet.
-\[{M_{sun}}\] is the mass of the sun.
-r is the size of orbit.
-v is speed or the orbital speed of the planet.
On solving the equation (i), we get
\[v = \sqrt {\dfrac{{G{M_{sun}}}}{r}} \]…………… (ii)
Now, calculation for the expression of time period (T)
Since, \[T = \dfrac{{2\pi r}}{v}\]
On substituting the value of v from equation (ii), in the above expression, We get
\[T = \dfrac{{2\pi r}}{{\sqrt {\dfrac{{G{M_{sun}}}}{r}} }}\]
\[ \Rightarrow T = 2\pi \sqrt {\dfrac{{{r^3}}}{{G{M_{sun}}}}} \]…………… (iii)
On squaring both sides in equation (iii), we get
\[{T^2} = \dfrac{{4{\pi ^2}{r^3}}}{{G{M_{sun}}}}\]

Note:
The derivation of Kepler's third law is one of the special cases of the circular orbits \[\left( {{T^2} \propto {r^3}} \right)\]. Sir Isaac Newton was able to show that the same relationship holds for an elliptical orbit, with the orbit radius r is replaced by semi-major axis a.