Question

Calculate the magnetic field at the center of a coil in a form of a square of side $ 2a $ carrying current $ I $ .

Answer 1

Hint: First we need to draw the given setup and observe its geometry to try and fit it into a direct formula that we know of to find the magnetic field at a point. Once we find the magnetic field at the center from one side, we can use the properties of symmetry to calculate the net magnetic field.

Formula used
 $ B = \dfrac{{{\mu _0}I}}{{4\pi r}}(\sin {\theta _1} + \sin {\theta _2}) $
where, $ B $ is the magnetic field,
 $ r $ is the distance between the current carrying conductor and the point where the magnetic field is to be found, and
 $ {\theta _1} $ and $ {\theta _2} $ are the subtending angles at the point where the magnetic field is to be found, from the two ends of the conductor.

Complete Step by step solution
The configuration of the setup is given below:

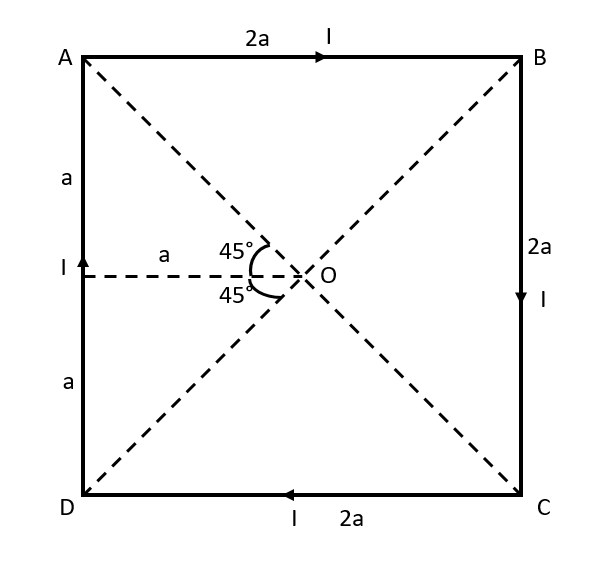
A specific direction of the current is not mentioned hence we can take the flow of current to be through any direction. Here we have taken the direction clockwise.
When we apply the right hand rule on all four sides of the current carrying wire, we can see that the magnetic field is directed into the plane at the center of the square, i.e., the point $ O $ .
Now, let us consider the side $ AD $ of the square to evaluate the magnetic field at the center of the square, $ O $ due to the current passing through the side $ AD $ .
We know that the general expression for the magnetic field, say $ B $ at a distance $ r $ from a straight current carrying conductor, subtending angles $ {\theta _1} $ and $ {\theta _2} $ at the point from the two ends of the conductor, is given as,
 $ B = \dfrac{{{\mu _0}I}}{{4\pi r}}(\sin {\theta _1} + \sin {\theta _2}) $
From the given figure we have the current provided as $ I $ , the distance between the point and the current carrying conductor as $ a $ , and $ {\theta _1} $ and $ {\theta _2} $ both as $ {45^\circ } $ .
Substituting these values in the above equation we get,
 $ B = \dfrac{{{\mu _0}I}}{{4\pi a}}(\sin {45^\circ } + \sin {45^\circ }) $
 $ \Rightarrow B = \dfrac{{{\mu _0}I}}{{4\pi a}}(2\sin {45^\circ }) $
We know that $ \sin {45^\circ } = \dfrac{1}{{\sqrt 2 }} $
 $ \therefore B = \dfrac{{{\mu _0}I}}{{4\pi a}}\dfrac{2}{{\sqrt 2 }} $
 $ \Rightarrow B = \dfrac{{\sqrt 2 {\mu _0}I}}{{4\pi a}} $
This is the field at the center of the square due to one side, $ AD $ .
But, due to symmetry, all other sides have the same magnetic field at the center of the square.
Therefore, the net magnetic field can be given as,
 $ {B_{net}} = 4B = 4 \times \dfrac{{\sqrt 2 {\mu _0}I}}{{4\pi a}} $
 $ \Rightarrow {B_{net}} = \dfrac{{\sqrt 2 {\mu _0}I}}{{\pi a}} $
This is the net magnetic field at the center of a square coil of the side $ 2a $ carrying current $ I $ .

Note
Keeping the geometry of the configuration in mind, we can solve a lot of problems like this one of electrostatics and magnetostatics very easily. Observe the symmetry of the setup very carefully and use it to reduce calculation very efficiently.