Question

Calculate the equivalent resistance between a and b of the following network of conductors.

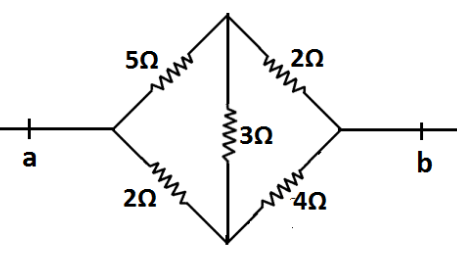
A. $4\Omega $
B. $5\Omega $
C. $3\Omega $
D. $2\Omega $

Answer 1

Hint:We can clearly see that the given circuit is the Wheatstone bridge circuit. We will first determine whether this circuit is balanced or unbalanced. After then, we will calculate the equivalent resistance based on the type of the bridge, balanced or unbalanced.

Complete step by step answer:
Let us first determine whether the given circuit is balanced or unbalanced.The ratio of the resistances on the left hand arms is $\dfrac{5}{2}$ and the ratio of the resistances on the right arms is $\dfrac{2}{4} = \dfrac{1}{2}$. As these both are not equal, the given Wheatstone bridge is unbalanced.

Now, we will find the equivalent resistance of this network step by step.Our first step is to convert the delta network to star network.As shown in figure, three resistances of $5\Omega $, $2\Omega $ and $3\Omega $ forms delta connection. So, we will convert this delta connection into a star connection of three resistances $P\Omega $, $Q\Omega $ and $R\Omega $ as shown in the figure.

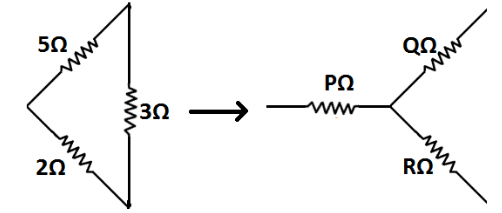
Now, we will find the resistances $P\Omega $, $Q\Omega $ and $R\Omega $ by using the rules of conversion from delta to star conversion.
$ \Rightarrow P = \dfrac{{5 \times 2}}{{5 + 2 + 3}} = \dfrac{{10}}{{10}} = 1\Omega $
$ \Rightarrow Q = \dfrac{{5 \times 3}}{{5 + 2 + 3}} = \dfrac{{15}}{{10}} = 1.5\Omega $
$ \Rightarrow R = \dfrac{{2 \times 3}}{{5 + 2 + 3}} = \dfrac{6}{{10}} = 0.6\Omega $
Thus, our main circuit will become as shown in the following figure.

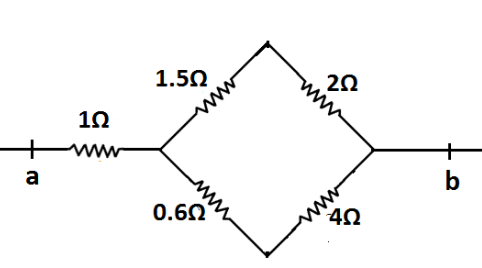
From the figure it is clear that resistances $1.5\Omega $ and $2\Omega $ are in series connection.We know that the equivalent resistance of two resistances connected in series is given by ${R_{eq}} = {R_1} + {R_2}$
Therefore, the equivalent resistance of $1.5\Omega $ and $2\Omega $ is $1.5 + 2 = 3.5\Omega $
Similarly, the equivalent resistance of $0.6\Omega $ and $4\Omega $ is $0.6 + 4 = 4.6\Omega $
Thus, our main circuit will become as shown in the following figure.

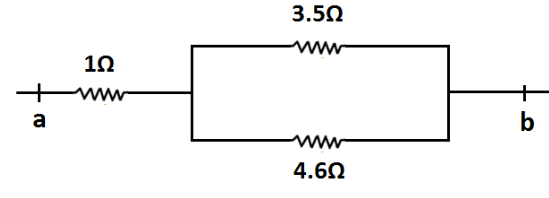
From the figure it is clear that resistances $3.5\Omega $ and $4.6\Omega $ are in parallel connection.We know that the equivalent resistance of two resistances connected in parallel is given by \[{R_{eq}} = \dfrac{{{R_1}{R_2}}}{{{R_1} + {R_2}}}\]
Therefore, the equivalent resistance of $3.5\Omega $ and $4.6\Omega $ is $\dfrac{{3.5 \times 4.6}}{{3.5 + 4.6}} = 1.99\Omega $

Now, our main circuit will become as shown in the following figure.Here, resistances $1\Omega $ and $1.99\Omega $ are in series connection.Therefore, the equivalent resistance of $1\Omega $ and $1.99\Omega $ is $1 + 1.99 = 2.99 \approx 3\Omega $

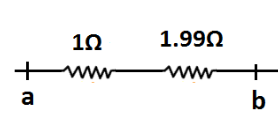
Here, resistances $1\Omega $ and $1.99\Omega $ are in series connection.Therefore, the equivalent resistance of $1\Omega $ and $1.99\Omega $ is $1 + 1.99 = 2.99 \approx 3\Omega $.
Finally, our circuit will be as shown in the following figure.

Thus, the equivalent resistance between a and b of the given network of conductors is $3\Omega $ .

Hence, option C is the right answer.

Note:In this type of question where the Wheatstone circuit is given, it is important to know if it is balanced or unbalanced. Here, the given circuit is unbalanced, therefore we have first converted the delta connection to star connection. And then, we have applied the laws of equivalent resistance for series and parallel connections to get our final answer.