Question

Box $A$ contains $3$ red and $2$ black balls. Box $B$ contains $2$ red and $3$ black balls. One ball is drawn at random from box $A$ and placed in box $B$. Then one ball is drawn at random from the box $B$ and placed in $A$. The probability that the composition of balls in the two boxes remains unaltered is
A: $\dfrac{9}{{30}}$
B: $\dfrac{4}{{15}}$
C: $\dfrac{{17}}{{30}}$
D: $\dfrac{{16}}{{30}}$

Answer 1

Hint: First, consider the red ball is transferred from box $A$ to box $B$ and then consider black ball is transferred from box $A$ to box $B$. Consider the same with respect to box $B$. Then find the probability of all to arrive at the required answer.

Complete step-by-step answer:
Below diagram shows the two boxes which contain red and black balls.

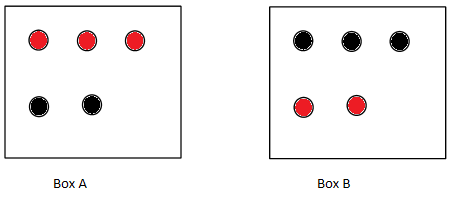
First, we take some cases to find the probability.
Case A: here, let the red ball be transferred from box $A$ to box $B$.
Case B: Here, the black ball is transferred from box $A$ to box $B$.
Case C: here, the red ball is transferred from box $B$ to box $A$.
Case D: here, the black ball is transferred from box $B$ to box $A$.
Now, we will find the probability of the above cases.
By using the probability formula, given below we find the required probability.
$P(A) = \dfrac{{n(A)}}{n}$
Where $P(A)$ denotes the probability of A
$n(A)$ is the number of occurrences of A or the number of favorable outcomes.
$n$ is the total number of possible outcomes or the sample space.
Now, in box A we have $3$ red balls out of $5$ balls so probability can be written as $P(A) = \dfrac{3}{5}$
And we have $2$ black balls in box A so this can be written as $P(B) = \dfrac{2}{5}$ .
After transferring balls from box A to box B we can write as below,
$P\left( {\dfrac{C}{A}} \right) = \dfrac{3}{6}$ and $P\left( {\dfrac{D}{B}} \right) = \dfrac{4}{6}$
Now, to find the probability of composition of balls that remains unaltered are
$P = P(A) \times P\left( {\dfrac{C}{A}} \right) + P(B) \times P\left( {\dfrac{D}{B}} \right)$
$ = \dfrac{3}{5} \times \dfrac{3}{6} + \dfrac{2}{5} \times \dfrac{4}{6}$
Taking L.C.M, we get
$ = \dfrac{{9 + 8}}{{30}}$
$ = \dfrac{{17}}{{30}}$
The probability of composition of balls that remains unaltered is $\dfrac{{17}}{{30}}$. Therefore, the option C is correct.

Note: In probability questions one thing you need to learn is observation and analysation. When taking the sample space and the number of favorable outcomes we should take care that we are taking the correct value otherwise it will lead to the wrong answer.