Question

$\begin{align}
  & If\text{ }ABCDE\text{ is a pentagon, then }\overrightarrow{AB}\text{ + }\overrightarrow{AE}\text{ +}\overrightarrow{\text{ }BC}\text{ +}\overrightarrow{\text{ }DC}\text{ + }\overrightarrow{ED}\text{ + }\overrightarrow{AC}\text{ equals} \\
 & \text{A}\text{. 3}\overrightarrow{\text{AD}} \\
 & \text{B}\text{. 3}\overrightarrow{AC} \\
 & \text{C}\text{. 3}\overrightarrow{BE} \\
 & \text{D}\text{. 3}\overrightarrow{CE} \\
\end{align}$

Answer 1

Hint: In the given question we have to find out sum of some vector. So, we have to know that how we can do the addition of vector and we should know the meaning of vector. A vector is a quantity which has both, that is magnitude as well as direction and which obey triangle rule of addition. Triangle rule of addition says that in a triangle if we add the sides of triangle in cyclic order the sum is zero. So, if ABC is a triangle then according to the triangle rule of addition, we can write $\overrightarrow{AB}\text{ }+\text{ }\overrightarrow{BC}\text{ }+\text{ }\overrightarrow{CA}\text{ }=\overrightarrow{\text{ }0}$. Also $\overrightarrow{AB}\text{ }=\text{ }-\overrightarrow{BA}$. In the given we have to add $\overrightarrow{AB}\text{ }+\overrightarrow{\text{ }AE}\text{ }+\text{ }\overrightarrow{BC}\text{ }+\text{ }\overrightarrow{DC}\text{ }+\text{ }\overrightarrow{ED}\text{ }+\text{ }\overrightarrow{AC}$so here we add two vector as $\overrightarrow{AB}\text{ }+\text{ }\overrightarrow{BC}$and $\overrightarrow{AE}\text{ }+\text{ }\overrightarrow{ED}$ so that we get third side of corresponding triangle and them move further.

Complete step-by-step solution:
Let ABCDE is a pentagon and we have to find $\overrightarrow{AB}\text{ }+\text{ }\overrightarrow{AE}\text{ }+\text{ }\overrightarrow{BC}\text{ }+\overrightarrow{\text{ }DC}\text{ }+\text{ }\overrightarrow{ED}\text{ }+\text{ }\overrightarrow{AC}$

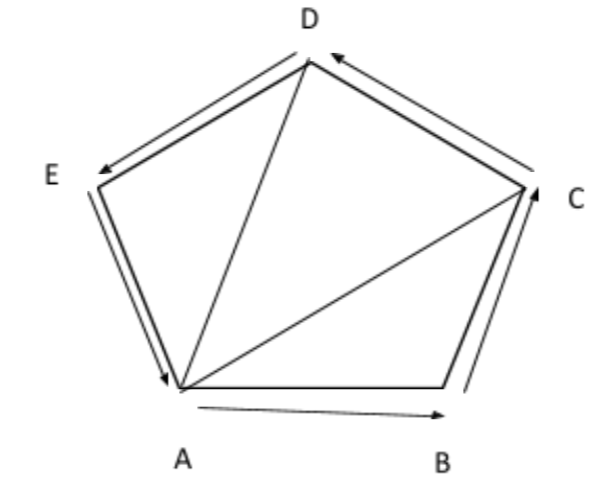
Consider the triangle ABC, we can write
$\overrightarrow{AB}\text{ }+\text{ }\overrightarrow{BC}\text{ }+\text{ }\overrightarrow{CA}=0$
Here we use triangle law of addition, so we can write
$\begin{align}
  & \overrightarrow{AB}\text{ }+\text{ }\overrightarrow{BC}=\text{ }-\overrightarrow{CA} \\
 & \overrightarrow{AB}\text{ }+\text{ }\overrightarrow{BC}\text{ }=\text{ }\overrightarrow{AC}------(a) \\
\end{align}$
Now in triangle AED we again use triangle law of addition so, we can write
\[\begin{align}
  & \overrightarrow{AE}\text{ }+\text{ }\overrightarrow{ED}\text{ }+\text{ }\overrightarrow{DA}\text{ }=\text{ }\overrightarrow{0} \\
 & \overrightarrow{AE\text{ }}+\text{ }\overrightarrow{ED}=-\overrightarrow{DA} \\
 & \overrightarrow{AE}\text{ }+\text{ }\overrightarrow{ED}=\text{ }\overrightarrow{AD}-----(b) \\
\end{align}\]
Again, we consider triangle ACD and we use here again triangle rule of addition, so, we can write
\[\begin{align}
  & \overrightarrow{AC}\text{ }+\text{ }\overrightarrow{CD}\text{ }+\text{ }\overrightarrow{DA}=\text{ }0 \\
 & \overrightarrow{AC}\text{ }+\text{ }\overrightarrow{CD}\text{ }=\text{ }-\overrightarrow{DA} \\
 & \overrightarrow{AC}\text{ }+\text{ }\overrightarrow{CD}\text{ }=\text{ }\overrightarrow{AD}------(c) \\
\end{align}\]
Now we do here$(a)+(b)+(c)$, so we can write
\[\overrightarrow{AB}\text{ }+\text{ }\overrightarrow{BC}\text{ }+\text{ }\overrightarrow{AE}\text{ }+\text{ }\overrightarrow{ED}\text{ }+\text{ }\overrightarrow{AC}\text{ }+\text{ }\overrightarrow{CD}\text{ }=\overrightarrow{AC}\text{ }+\text{ }\overrightarrow{AD}\text{ }+\text{ }\overrightarrow{AD}\]
Now we add $\overrightarrow{DC}$both side we can write
$\overrightarrow{AB}\text{ }+\text{ }\overrightarrow{BC}\text{ }+\text{ }\overrightarrow{AE}\text{ }+\text{ }\overrightarrow{ED}\text{ }+\text{ }\overrightarrow{AC}\text{ }+\text{ }\overrightarrow{CD}\text{ }+\text{ }\overrightarrow{DC}\text{ }=\text{ }\overrightarrow{AC}\text{ }+\text{ }\overrightarrow{AD}\text{ }+\text{ }\overrightarrow{AD}\text{ }+\text{ }\overrightarrow{DC}$
Taking $\overrightarrow{CD}$to right hand side we can write
\[\begin{align}
  & \overrightarrow{AB}\text{ }+\text{ }\overrightarrow{BC}\text{ }+\text{ }\overrightarrow{AE}\text{ }+\text{ }\overrightarrow{ED}\text{ }+\text{ }\overrightarrow{AC}\text{ }+\overrightarrow{\text{ }DC}\text{ }=\text{ }\overrightarrow{AC}\text{ }+\text{ }\overrightarrow{AD}\text{ }+\text{ }\overrightarrow{AD}\text{ }+\text{ }\overrightarrow{DC}\text{ }-\text{ }\overrightarrow{CD} \\
 & \overrightarrow{AB}\text{ }+\text{ }\overrightarrow{BC}\text{ }+\text{ }\overrightarrow{AE}\text{ }+\text{ }\overrightarrow{ED}\text{ }+\text{ }\overrightarrow{AC}\text{ }+\text{ }\overrightarrow{DC}\text{ }=\text{ }\overrightarrow{AC}\text{ }+\text{ }\overrightarrow{AD}\text{ }+\text{ }\overrightarrow{AD}\text{ }+\text{ }\overrightarrow{DC}\text{ }+\text{ }\overrightarrow{DC} \\
 & \overrightarrow{AB}\text{ }+\text{ }\overrightarrow{BC}\text{ }+\text{ }\overrightarrow{AE}\text{ }+\text{ }\overrightarrow{ED}\text{ }+\text{ }\overrightarrow{AC}\text{ }+\text{ }\overrightarrow{DC}\text{ }=\text{ }\overrightarrow{AC}\text{ }+\text{ }2(\overrightarrow{AD}\text{ }+\text{ }\overrightarrow{DC}) \\
\end{align}\]
Now in triangle ADC we have
$\begin{align}
  & \overrightarrow{AD}\text{ }+\text{ }\overrightarrow{DC}\text{ }+\text{ }\overrightarrow{CA}\text{ }=\text{ }\overrightarrow{0} \\
 & \overrightarrow{AD}\text{ }+\text{ }\overrightarrow{DC}\text{ }=\text{ }-\overrightarrow{CA} \\
 & \overrightarrow{AD}\text{ }+\text{ }\overrightarrow{DC}\text{ }=\text{ }\overrightarrow{AC}-----(d) \\
\end{align}$
Now we can substitute the value of $\overrightarrow{AD}\text{ }+\text{ }\overrightarrow{DC}$ from equation $(d)$ we can write
$\begin{align}
  & \overrightarrow{AB}\text{ }+\text{ }\overrightarrow{BC}\text{ }+\text{ }\overrightarrow{AE}\text{ }+\text{ }\overrightarrow{ED}\text{ }+\text{ }\overrightarrow{AC}\text{ }+\text{ }\overrightarrow{DC}\text{ }=\text{ }\overrightarrow{AC}\text{ }+\text{ }2(\overrightarrow{AC}) \\
 & \overrightarrow{AB}\text{ }+\text{ }\overrightarrow{BC}\text{ }+\text{ }\overrightarrow{AE}\text{ }+\text{ }\overrightarrow{ED}\text{ }+\text{ }\overrightarrow{AC}\text{ }+\text{ }\overrightarrow{DC}\text{ }=\text{ }3\overrightarrow{AC} \\
\end{align}$
Hence, option B is correct.

Note: The addition of vector can be done by the rule of parallelogram also. According to it if $\overrightarrow{a}$ and $\overrightarrow{b}$ are two vectors which is to be added we form a parallelogram by using $\overrightarrow{a}$ and $\overrightarrow{b}$ as the side of parallelogram. One of the diagonals (main) so formed is the addition of vectors.

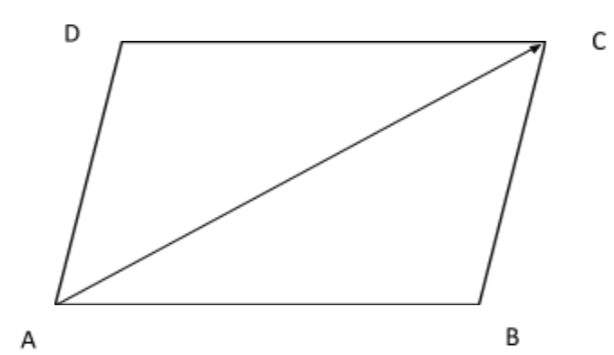
In the above diagram AC is the diagonal of the parallelogram ABCD. As per the addition rule of parallelogram we can write
$\begin{align}
  & \overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{BC} \\
 & \overrightarrow{AC}=\overrightarrow{a}+\overrightarrow{b} \\
\end{align}$
It should be noted here the parallel translation of vector does not change its value.