Question

At the corners of an equilateral triangle of side $a\left( 1\text{ metre} \right)$, three point charges are placed (each of $0.1C$). If this system is supplied energy at the rate of $1kW$ , then calculate the time required to move one charge to the midpoint of the line joining the other two.

A) $50\text{ }h$
B) $60\text{ }h$
C) $\text{48 }h$
D) $54\text{ }h$

Answer 1

Hint: This problem can be solved by finding out the electric potential energy of the system in the initial and final state. Then we can find the difference in these energies and that will be the required energy that has to be supplied to the system. With the information given in the question about the rate of energy being supplied to the system we will get the required time for the change.

Formula used:
The electric potential energy between a pair of charges $Q$ and $q$ is given by
$\dfrac{KQq}{R}$ --(1)
where $R$ is the distance between the two point charges and $K=9\times {{10}^{9}}kg.{{m}^{3}}{{s}^{-2}}{{C}^{-2}}$ is the universal electric constant.

Complete step-by-step answer:
As explained in the hint, we will find the difference between the initial and final states of the system.
The electric potential energy between a pair of charges $Q$ and $q$ is given by $\dfrac{KQq}{R}$ --(1) where $R$ is the distance between the two point charges and $K=9\times {{10}^{9}}kg.{{m}^{3}}{{s}^{-2}}{{C}^{-2}}$ is the universal electric constant.
Let us analyze the initial state of the system of three charges.

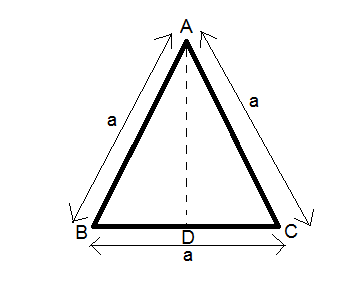
It is given that all the charges are equal $\left( 0.1C \right)$. Hence, let all the charges be $Q$. The distance between each charge is $a$.
Therefore, the initial energy of the system $\left( {{E}_{i}} \right)$ will be nothing but the sum of the electric potential energy of each pair of charges.
$\therefore {{E}_{i}}=K\dfrac{{{Q}_{A}}{{Q}_{B}}}{{{R}_{AB}}}+K\dfrac{{{Q}_{A}}{{Q}_{C}}}{{{R}_{AC}}}+K\dfrac{{{Q}_{B}}{{Q}_{C}}}{{{R}_{BC}}}$ --(2) where ${{Q}_{A}},{{Q}_{B}},{{Q}_{C}}$ symbolizes the charges at $A,B,C$ respectively. ${{R}_{AB}},{{R}_{BC}},{{R}_{AC}}$ are the distances between A and B, B and C, and C and A respectively.
Now, according to the question and figure, ${{Q}_{A}}={{Q}_{B}}={{Q}_{C}}=Q=0.1C$ ${{R}_{AB}}={{R}_{BC}}={{R}_{AC}}=a$
Putting the above values in (2), we get,
$\therefore {{E}_{i}}=K\dfrac{QQ}{a}+K\dfrac{QQ}{a}+K\dfrac{QQ}{a}+=3K\dfrac{{{Q}^{2}}}{a}$ --(3)
Now, in the final state of the system, one of the charges is in the midpoint of the line joining the other two. Let us bring charge B, to the midpoint of AC. Hence, the system will look like the following figure,

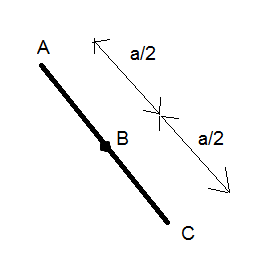
Therefore, the final energy of the system $\left( {{E}_{f}} \right)$ will be nothing but the sum of the electric potential energy of each pair of charges.
$\therefore {{E}_{f}}=K\dfrac{{{Q}_{A}}{{Q}_{B}}}{{{R}_{AB}}}+K\dfrac{{{Q}_{A}}{{Q}_{C}}}{{{R}_{AC}}}+K\dfrac{{{Q}_{B}}{{Q}_{C}}}{{{R}_{BC}}}$ --(4) where ${{Q}_{A}},{{Q}_{B}},{{Q}_{C}}$ symbolizes the charges at $A,B,C$ respectively. ${{R}_{AB}},{{R}_{BC}},{{R}_{AC}}$ are the distances between A and B, B and C, and C and A respectively.
Now, according to the question and figure, ${{Q}_{A}}={{Q}_{B}}={{Q}_{C}}=Q=0.1C$ ${{R}_{AB}}={{R}_{BC}}=\dfrac{a}{2}$ ${{R}_{AC}}=a$
Hence, putting the above values in (4), we get, ${{E}_{f}}=K\dfrac{QQ}{\dfrac{a}{2}}+K\dfrac{QQ}{a}+K\dfrac{QQ}{\dfrac{a}{2}}=5K\dfrac{{{Q}^{2}}}{a}$ --(5)
Hence, the change in energy of the system $\Delta E$ is $\Delta E={{E}_{f}}-{{E}_{i}}$ Using (3) and (5), we get, $\Delta E=5K\dfrac{{{Q}^{2}}}{a}-3K\dfrac{{{Q}^{2}}}{a}=2K\dfrac{{{Q}^{2}}}{a}$ --(6)
Now, according to the question, $Q=0.1C$ $a=1m$ Therefore, putting these values in (6), we get, $\Delta E=2\times 9\times {{10}^{9}}\times \dfrac{0.1\times 0.1}{1}=18\times {{10}^{7}}J$ --(7)
Now, according to the question, energy is being supplied to the system at a rate of $1kW$. Therefore, the time required for the complete state change of the system will be nothing but, $\text{Total time required = }\dfrac{\text{Total energy required}}{\text{Rate of supply of energy}}$
Hence, using (7), we get, $\text{Total time taken = }\dfrac{18\times {{10}^{7}}J}{{{10}^{3}}J/s}=18\times {{10}^{4}}s$ [$\left( \because 1kW={{10}^{3}}W \right)$,$\left( 1W=1J/s \right)$] $=\dfrac{18\times {{10}^{4}}}{3600}=50hr$ $\left( \because 1hr=3600s \right)$
Hence, the time required is $50hr$. Therefore, the correct option is A) $50\text{ }h$

Note: Students often make the mistake of finding out the electric potential energy of each charge individually, however they must understand that the electric potential energy is for a pair of charges due to the effects of which there is a potential energy on each charge in the pair. If students proceed to get the electric potential energy for each individual charge, they will end up with double the energy change and hence double the answer of the time required, that is, the answer of this question.