Question

(a)State Snell’s law for refraction of light.
(b)A concave mirror forms two times magnified and real images of an object placed at 15cm from its pole. Determine the distance of image from the mirror and focal length of the mirror.

Answer 1

Hint: Snell’s law talks about the relation between incidence and refraction angles and is defined by the ratio of $\dfrac{{\sin {\theta _2}}}{{\sin {\theta _1}}} = \dfrac{{{v_2}}}{{{v_1}}} = \dfrac{{{n_1}}}{{{n_2}}}$. In the second part we need to find the distance of distance of the image from the pole, as the distance of the object from the pole is given and the magnification is also given, so we can use $m = \dfrac{{ - v}}{u}$, to calculate the image distance from the pole and the focal length can be calculated by $\dfrac{1}{v} + \dfrac{1}{u} = \dfrac{1}{f}$.

Complete step by step answer:
a) The light normally bends, or refracts, as light passes from one medium to another. The refraction law gives us a way to estimate how much bend is produced and it is defined by Snell’s law.
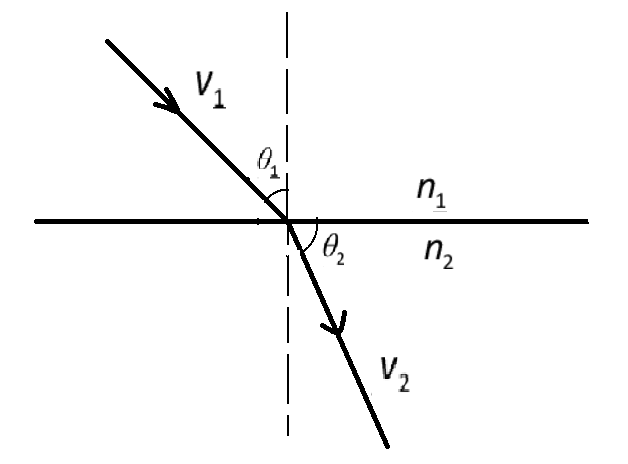
The Snell’s law is a law used to explain the relationship between incidence and refraction angles when applied to light or other waves moving across a boundary between two distinct non-opaque materials, such as water, glass or air.
Snell's law states that the sin ratio of incidence and refraction angles is equal to the ratio of phase velocities of all media or identical to the inverse ratio of refraction indices and is given by:
$\dfrac{{\sin {\theta _2}}}{{\sin {\theta _1}}} = \dfrac{{{v_2}}}{{{v_1}}} = \dfrac{{{n_1}}}{{{n_2}}}$, where ${\theta _1}$ is the angle of incidence and ${\theta _2}$ is the angle of refraction, ${v_1}$ is the speed of light in the first medium and ${v_2}$ is the speed of light in the second medium, and \[{n_1}\] and ${n_2}$ are the refractive index of medium one and medium two respectively.

b) It is given that the concave mirror forms two times magnified and real images of an object placed at 15cm from its pole.
So, $u = 15\,{\text{cm}}$ and as the image is real and the magnification is two times, therefore $m = - 2$.
Now as,
$m = \dfrac{{ - v}}{u}$
Substitute, $u = 15\,{\text{cm}}$ and $m = - 2$ in the above formula.
$- 2 = \dfrac{{ - v}}{{15}} \\ - v = - 2\left( {15} \right) \\ v = 30\,{\text{cm}} \\ $
Therefore, the image formed is 30 cm away from the pole.
Now, as focal length is calculated by $\dfrac{1}{v} + \dfrac{1}{u} = \dfrac{1}{f}$.
Now, substitute $v = 30\,{\text{cm}}$ and $u = 15\,{\text{cm}}$ in the formula $\dfrac{1}{v} + \dfrac{1}{u} = \dfrac{1}{f}$ and calculate the value of focal length.
$ \dfrac{1}{v} + \dfrac{1}{u} = \dfrac{1}{f} \\ \dfrac{1}{{30}} + \dfrac{1}{{15}} = \dfrac{1}{f} \\\dfrac{1}{f} = \dfrac{{1 + 2}}{{30}} \\\dfrac{1}{f} = \dfrac{3}{{30}} \\ \dfrac{1}{f} = \dfrac{1}{{10}} \\ f = 10\,{\text{cm}} \\ $

Therefore, the focal length of the mirror is 10 cm.

Note: This is a question is of ray optics, Snell’s law is the basis of ray optics, it is defined for both reflection and refraction and the second part is focusing on the image formation where we need to find the image distance using $m = \frac{{ - v}}{u}$ and we can calculate focal length using the formula $\frac{1}{v} + \frac{1}{u} = \frac{1}{f}$.