Question

As x increases from $\dfrac{\pi }{4}$ to $\dfrac{3\pi }{4}$ , $\left| \sin \left( 2x \right) \right|$
(a) Always increases
(b) Always decreases
(c) Increases then decreases
(d) Decreases then increases
(e) Stay constant$$$$

Answer 1

Hint: In order to solve this problem, we need to find a way to plot the function. The modulus of the function makes all the negative terms positive. Also, we can either draw the function in radians scale or convert the required range in degrees we can change by multiplying by the factor of $\dfrac{180}{\pi }$.

Complete step by step answer:
Let’s first understand the question.
We are given to find the behaviour of the function in a certain domain.
It would be easy if we plot the function.
We have asked to plot the function of $\left| \sin \left( 2x \right) \right|$ ,
Let’s start with plotting the function of $\sin x$ .

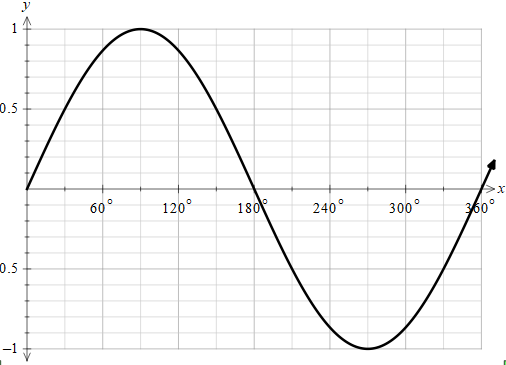
As we can see that the maximum value of the graph is between +1 and -1.
Now, let's draw the graph of $\sin 2x$ .

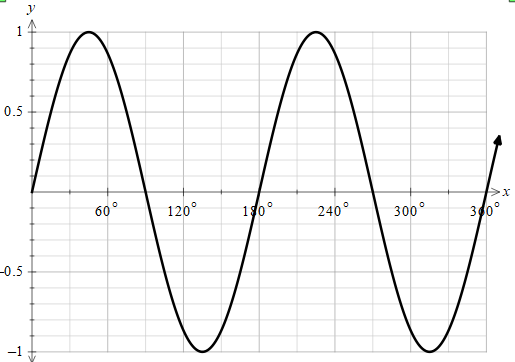
As we can see, that by comparing with the $\sin x$ graph looks shrunk. This is because of factor 2. Whenever any constant multiplies with the variable directly it either stretches or expands depending on the constant.
Let's draw the function of $\left| \sin 2x \right|$ .
The main function of the modulus is to make all the negative terms positive.
Hence, the graph looks like as below,

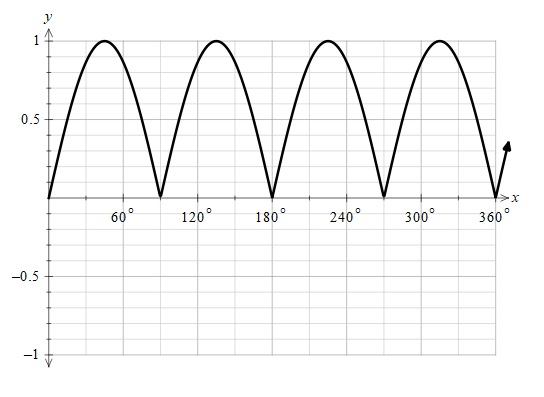
All the portion from the negative half cycle is converted into positive.
Now, we need to find the behaviour of the graph in the range $\dfrac{\pi }{4}$ to $\dfrac{3\pi }{4}$ .
The range we have given is in radians and we have the graphs in degrees. So, now we have to convert the radians into degrees.
For converting radians to degrees, we have to multiply by the factor of $\dfrac{180}{\pi }$ .
Therefore, converting $\dfrac{\pi }{4}$ into degrees we get,
$\dfrac{\pi }{4}\times \dfrac{180}{\pi }={{45}^{\circ }}$ .
Now, converting $\dfrac{3\pi }{4}$ into degrees we get,
$\dfrac{3\pi }{4}\times \dfrac{180}{\pi }={{135}^{\circ }}$ .
So, now we have to find the behaviour of the function from the range ${{45}^{\circ }}$ to ${{135}^{\circ }}$ .

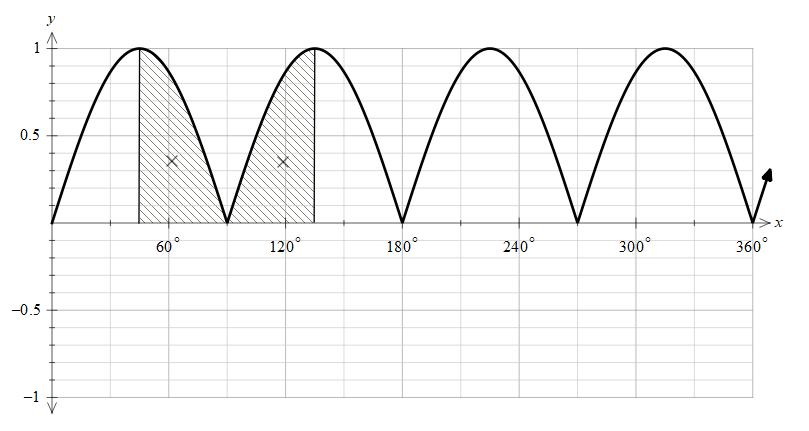
The shaded region is the range from ${{45}^{\circ }}$ to ${{135}^{\circ }}$ .
As we can see that the function first decreases and then increases.

So, the correct answer is “Option d”.

Note: In this problem, we must understand how to plot the graph. Whenever any constant multiplies with the variable directly in sine or cosine function it either stretches or expands depending on the constant. Also, the sin is an oscillating function and this function will never be a constant. So, option (e) is eliminated.