Question

Area enclosed between the curves $|y|=1-{{x}^{2}}$ and ${{x}^{2}}+{{y}^{2}}=1$ is.
(a) $\dfrac{3\pi -14}{3}\; \text{sq. units}$
(b) $\dfrac{\pi -8}{3}\; \text{sq. units}$
(c) $\dfrac{2\pi -8}{3}\; \text{sq. units}$
(d) None of these

Answer 1

Hint: By using normal modulus properties remove the modulus. Now find the graph of these two graphs. Then find intersection points of both. By this draw all graphs in one graph paper. Now shade the bounded region. Now subtract the function above and the function below integrate this difference to get the area bounded.

Complete step-by-step solution -
Given curves in the question can be written as:
${{x}^{2}}+{{y}^{2}}=1$
By basic knowledge of conics, we say that ${{\left( x-g \right)}^{2}}+{{\left( x-n \right)}^{2}}={{r}^{2}}$ is a circle with radius r and centre at (g, n). So, this equation is a circle with radius 1, centre (0,0). The second equation given in the question, can be written as: $|y|=\left( 1-{{x}^{2}} \right)$.
To remove modulus, we can introduce the $\pm $ sign in the equation. By doing as said above, we get the equation:
$y=\pm \left( 1-{{x}^{2}} \right)$
We can get two equations from the above as:
$y=1-{{x}^{2}};\,\,y={{x}^{2}}-1$
As we can see, it is a 1-unit shift from (0,0). So, both equations pass through (0, 1), (-1,0), (1,0), (0, -1). So, these will be intersection points.
Now we will draw their curves.
Curves: -
${{x}^{2}}+{{y}^{2}}=1$

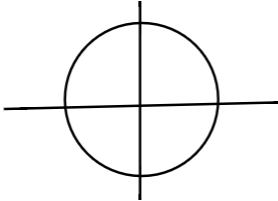
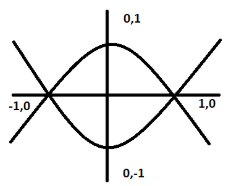
$y=\pm \left( 1-{{x}^{2}} \right)$

By combining both the curves and shading the bounded area:

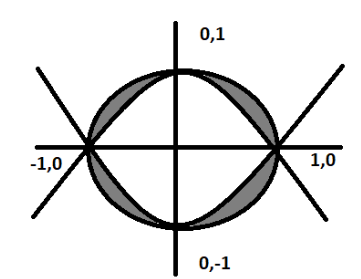
The area is present in all the four quadrants of the circle. By symmetry we say all the four areas are equal. So, if we calculate one area and multiply by 4, we get required area = 4×(first quadrant)…………..(i),
If f(x) is above g(x), the are founded from \[x={{x}_{1}}\] to \[x'={{x}_{2}}\]
Are bounded = \[\int\limits_{{{x}_{1}}}^{{{x}_{2}}}{f(x)-g(x)}\]
Here we have g(x)= $1-{{x}^{2}}$. We need to find f(x) that is a circle.
${{x}^{2}}+{{y}^{2}}=1$. So, the area of its first question is given by $\dfrac{A}{t}$, where A= area of circle = $\pi {{r}^{2}}$.
So, area of f(x)= $\dfrac{\pi {{\left( 1 \right)}^{2}}}{4}=\dfrac{\pi }{4}=\int\limits_{{{x}_{1}}}^{{{x}_{2}}}{_{f(x)}dx}$
So, the g(x) is integrated from 0 to 1= $\int\limits_{0}^{1}{1-{{x}^{2}}dx}$
By basic integration we can solve it as:
${{\left[ x-\dfrac{{{x}^{3}}}{3} \right]}^{1}}_{0}=1-\dfrac{1}{3}=\dfrac{2}{3}$
Area bounded = \[4\int\limits_{{{x}_{1}}}^{{{x}_{2}}}{f(x)}-g(x)dx=4\left( \dfrac{\pi }{4}-\dfrac{2}{3} \right)\]
By simplifying the above, we can say the total area as:
Area= $\dfrac{4\pi }{4}-\dfrac{8}{3}$
By taking least common multiple, we can say the area as:
Area= $\dfrac{3\pi -8}{3}$sq. units.
Therefore option (d) is correct.

Note: Be careful, if you do not observe intersection points you may substitute the $2^{nd}$ curve into the first one and solve the biquadratic equation to get 4 roots given by 4 intersection points or you can draw first from where you can see the points. After getting an area in first quadrants students forget to multiply 4 but it is a must to do step.