Question

An unknown resistance is put in one gap and a resistance of $60\Omega $ in the other gap of a meter bridge and null point is obtained. If unknown resistance is now shunted by a resistance $\dfrac{1}{9}$ of its value, calculate the known resistance which will give the same null point as before.

Answer 1

Hint: As a first step, you could recall the expression for balanced condition of a meter bridge. Now you could substitute accordingly as per initial conditions given in the question in that expression. Then you could do the same for the second part where the unknown resistance is shunted. Combining both, you will get the value of the resistance at the right gap in the second part.

Formula used: Balanced condition of the meter bridge,
$\dfrac{l}{\left( 100-l \right)}=\dfrac{P}{Q}$

Complete step by step answer:
In the question, we are given a meter bridge. In the left gap of the bridge, an unknown resistance is put and in the other gap we have a resistance of $60\Omega $ and a null point is obtained under these conditions. Now we are shunting the unknown resistance by a resistance $\dfrac{1}{9}th$ of its original value and we are asked to find the value of the known resistance such that we obtain the same null point as before.

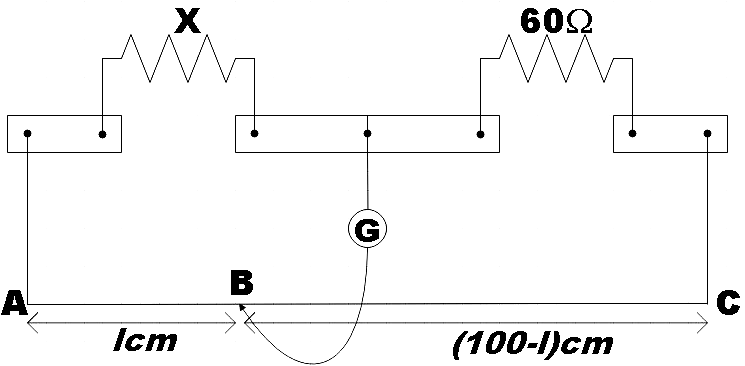
In the above meter bridge, the balance point or the null point is obtained at point B at a distance of $lcm$from the point A at the left end. We know that, the meter bridge is an application of the Wheatstone bridge whose balance point is given by,
$\dfrac{l}{\left( 100-l \right)}=\dfrac{X}{60\Omega }$ ……………………………………………………….. (1)
Now we are shunting the unknown resistance X by a resistance of $\dfrac{1}{9}th$ of its value, so the effective resistance at left gap now will be,
$X'=\dfrac{X\times \left( \dfrac{1}{9}X \right)}{X+\left( \dfrac{1}{9}X \right)}$
$\Rightarrow X'=\dfrac{\dfrac{{{X}^{2}}}{9}}{\dfrac{10X}{9}}$
$\therefore X'=\dfrac{X}{10}$ …………………………………………………………… (2)

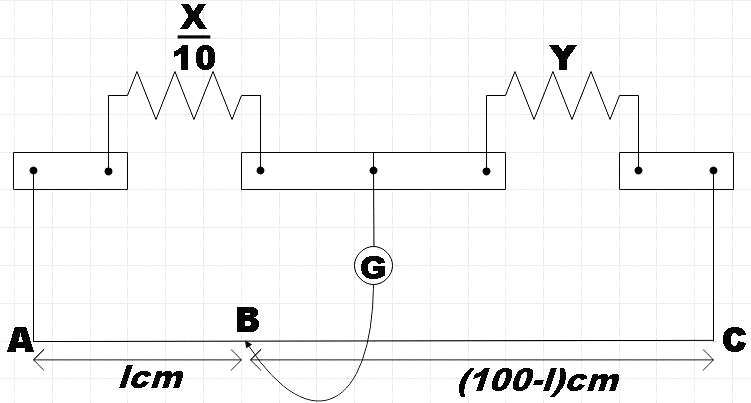
We are supposed to find the value of resistance Y such that the balance point is the same as before.
At balanced condition of the meter bridge,
$\dfrac{l}{\left( 100-l \right)}=\dfrac{\dfrac{X}{10}}{Y}$…………………………………….. (3)
Substituting (1) in (3), we get,
$\dfrac{X}{60}=\dfrac{X}{10Y}$
$\Rightarrow 10Y=60$
$\therefore Y=6\Omega $

Hence, we found the resistance of the resistor in the right gap to be $6\Omega $.

Note: You may have noticed the word null point or the balanced point in the solution. It is that point on the 1m length wire of the meter bridge where the galvanometer shows zero deflection. We know that the resistance of the wire depends on the dimensions, so, one possible error in the meter bridge will be due to the non-uniformity in the wire.