Question

An oil funnel of tin sheet consists of a cylindrical portion 10 cm. long attached to a frustum of a cone. If the total height is 22cm, diameter of the cylindrical portion is 8cm and the diameter of the top of the funnel is 18 cm, find the area of the tin required to make the funnel.
(a). 876.26 $c{{m}^{2}}$
(b). 657.26 $c{{m}^{2}}$
(c). 782.57 $c{{m}^{2}}$
(d). 982.26 $c{{m}^{2}}$

Answer 1

Hint: Split the funnel area into cylindrical part and Frustum part and use the formulae ‘CSA of cylinder $=\pi \times d\times h$’ and ‘CSA of frustum $=\pi \times \left( \dfrac{D}{2}+\dfrac{d}{2} \right)\times l$’ and add the outcomes to get the final answer.

Complete step-by-step answer:

To solve the above problem we have drawn a diagram of the funnel first so that we can understand the problem easily and can solve it by using the notations of the diagram.

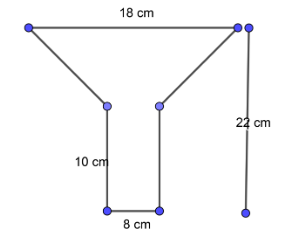
As we have constructed the diagram and gave measures to it as given in the question therefore we can write given values from diagram as follows,
Diameter of cylindrical base = d = 2r = 8 cm …………………………….. (1)
Height of cylindrical part = h = 10 cm …………………………….. (2)
As, Total height of funnel = 22 cm therefore the height of frustum will become,
Height of Frustum = H = 22 – 10 = 12 cm. …………………………….. (3)
Diameter of frustum top = D = 2R = 18 cm. …………………………….. (4)
Now we should know that area of tin required for making the funnel is equal to the curved surface area of funnel, and as the funnel is made up of cylinder and a frustum therefore we can write,
Area of tin required = Curved surface area of Cylinder + Curved surface area of Frustum.
Therefore, Area of tin required = CSA of cylinder + CSA of Frustum ……………………… (A)
Now we will find the CSA of both the parts separately,
To find the CSA of cylindrical part we should know the formula of CSA of cylinder which is given below,
Formula:
CSA of cylinder $=\pi \times d\times h$
If we put the values of equation (1) and (2) in above equation we will get,
CSA of cylinder $=\pi \times 8\times 10$
Therefore, CSA of cylinder $=80\pi $ $c{{m}^{2}}$…………………………… (5)
To find the CSA of Frustum part we should know the formula of CSA of frustum which is given below,
Formula:
CSA of frustum $=\pi \times \left( R+r \right)\times l$
As we know that the radius in half of diameter therefore,
CSA of frustum $=\pi \times \left( \dfrac{D}{2}+\dfrac{d}{2} \right)\times l$…………………………………….. (6)
Where ‘l’ is the slant height and which can be calculated by using formula given below,
$l=\sqrt{{{H}^{2}}+{{\left( R-r \right)}^{2}}}$
$\therefore l=\sqrt{{{H}^{2}}+{{\left( \dfrac{D}{2}-\dfrac{d}{2} \right)}^{2}}}$
If we put the values of equation (1), (3) and (4) we will get,
$\therefore l=\sqrt{{{12}^{2}}+{{\left( \dfrac{18}{2}-\dfrac{8}{2} \right)}^{2}}}$
$\therefore l=\sqrt{144+{{\left( 9-4 \right)}^{2}}}$
$\therefore l=\sqrt{144+{{\left( 5 \right)}^{2}}}$
$\therefore l=\sqrt{144+25}$
$\therefore l=\sqrt{169}$
$\therefore l=13$ cm
If we put the value of ‘I’ in equation (6) we will get,
CSA of frustum $=\pi \times \left( \dfrac{18}{2}+\dfrac{8}{2} \right)\times 13$
Therefore, CSA of frustum $=\pi \times \left( 9+4 \right)\times 13$
Therefore, CSA of frustum $=\pi \times 13\times 13$
Therefore, CSA of frustum $=169\pi $$c{{m}^{2}}$………………………………. (7)
Now, we will put the value of equation (5) and equation (7) in equation (A) we will get,
Area of tin required = CSA of cylinder + CSA of Frustum
Therefore, Area of tin required $=80\pi +169\pi $
Therefore, Area of tin required $=249\pi $
Therefore, Area of tin required $=782.25$$c{{m}^{2}}$
Therefore the correct answer in option (c).

Note: In the formula CSA of frustum $=\pi \times \left( \dfrac{D}{2}+\dfrac{d}{2} \right)\times l$, l is a slant height and not the height ‘H’ so be careful while calculating it otherwise you will get a wrong answer. Use the formula $l=\sqrt{{{H}^{2}}+{{\left( R-r \right)}^{2}}}$ to find the slant height in this case.