Question

An observer 1.5 m tall is 28.5 m away from a tower. The angle of elevation of the top of the tower from his/her eyes has measure 45 degrees. What is the height of the tower?
A. 28.5 m
B. 30 m
C. 27 m
D. 1.5 m

Answer 1

Hint: In order to solve this problem firstly draw the diagram then apply the concept of trigonometric angles in the triangles with the help of given data. Doing this will take you to the actual height of the tower.

Complete step-by-step answer:

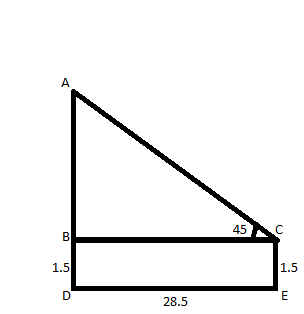
The diagram for solving this problem has been drawn above. Lengths are in meters and angles are in degrees.
CE is the height of man = 1.5 m
AD is the height of the tower = BD + AB = 1.5 + AB (As BD and CE are opposite sides of rectangle BDEC therefore BD = CE)
So, we have to find AD which is equals to 1.5 + AB ……(1)
So, if we find AB we can find AD from (1).
On considering triangle ABC from the figure we can say that,
tan 45 = 1 = $\dfrac{{{\text{AB}}}}{{{\text{BC}}}}$ ……(2)
We know that BC = DE =28.5 ($\because $ they are the opposite sides of the rectangle)
On putting the value of BC in (2) we get the equation as:
AB=(1)(28.5)=28.5
So, AB = 28.5
Height of the tower AD = 28.5 + 1.5 = 30 (From (1))
Hence, the height of the tower is 30 meters.
So, the correct option is B.

Note: In this type of problem students often make the mistake of excluding the height of the man in height of the tower.