Question

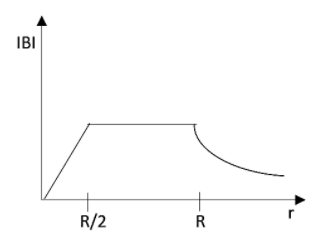
An infinitely conducting long hollow cylinder having an inner radius $\dfrac{R}{2}$ and outer radius $R$ is carrying a uniform current density along its length. The magnitude of the magnetic field, $\left| B \right|$ as a function of the distance $r$ from the axis is indicated using the figure,
A.

B.

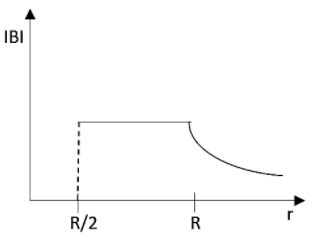
C.

D.

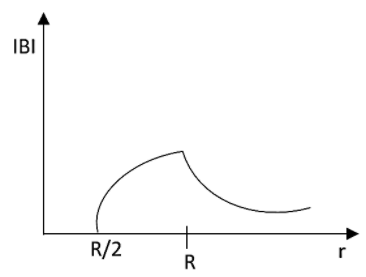
Answer 1

Hint: First of all consider the condition where the position is before $\dfrac{R}{2}$. Find the magnetic field over there. Then consider the region in between the $\dfrac{R}{2} < R$. Find the magnetic field in this region also. Then find the magnetic field after the radius also. And then using this information, plot the graph.

Complete answer:
First of all let us consider case 1.
In this case, we can write that,
$x < \dfrac{R}{2}$
Up to this position, the magnetic field is found to be zero.

Now let us check case number 2.
In this case we are taking the region from the half of the radius to the total of the radius. That is we can write that,
$\dfrac{R}{2}\le x < R$
According to Ampere’s circuital law, the line integral of the magnetic field around a closed loop is directly proportional to the current passing through the loop. This can be written mathematically as,
$\int{\vec{B}\cdot d\vec{l}}={{\mu }_{0}}I$
So let us apply this in the question.
$d\vec{l}=2\pi x$
As we all know, the current density is given by the equation,
$J=\dfrac{I}{A}$
Where $I$ be the current through the cylinder, $A$ be the area of the cylinder. Rearranging this equation will give,
$I=JA$
Where there will be the area of the cylinder except the region up to the half of the radius as that region is not discussed in this case.
That is,
$A=\pi {{x}^{2}}-\pi {{\left( \dfrac{R}{2} \right)}^{2}}$
Substituting this in the equation of current will give,
$I=\left[ \pi {{x}^{2}}-\pi {{\left( \dfrac{R}{2} \right)}^{2}} \right]J$
Substituting all these in the equation of ampere's circuital law,
\[\left| B \right|2\pi x={{\mu }_{0}}\left[ \pi {{x}^{2}}-\pi {{\left( \dfrac{R}{2} \right)}^{2}} \right]J\]
Simplifying and rearranging this equation will give,
\[\left| B \right|=\dfrac{{{\mu }_{0}}J}{2x}\left[ {{x}^{2}}-\pi \dfrac{{{R}^{2}}}{4} \right]\]
Now let us look at case 3.
That is the region,
\[x\ge R\]
Let us use the ampere’s circuital law in this region also.
$\int{\vec{B}\cdot d\vec{l}}={{\mu }_{0}}I$
Here,
\[d\vec{l}=2\pi x\]
Area can be taken as,
\[A=\pi {{R}^{2}}-\pi {{\left( \dfrac{R}{2} \right)}^{2}}\]
That is,
\[I=\left[ \pi {{R}^{2}}-\pi {{\left( \dfrac{R}{2} \right)}^{2}} \right]J\]
Substituting this in the equation will give,
\[\left| B \right|2\pi x={{\mu }_{0}}\left[ \pi {{R}^{2}}-\pi {{\left( \dfrac{R}{2} \right)}^{2}} \right]J\]
Simplifying this equation by cancelling the common terms and expanding the bracket will give,
\[\begin{align}
  & \left| B \right|2x={{\mu }_{0}}\left[ {{R}^{2}}-{{\left( \dfrac{R}{2} \right)}^{2}} \right]J \\
 & \Rightarrow \left| B \right|2x={{\mu }_{0}}\left[ {{R}^{2}}-\dfrac{{{R}^{2}}}{4} \right]J \\
 & \Rightarrow \left| B \right|2x={{\mu }_{0}}\left[ \dfrac{3{{R}^{2}}}{4} \right]J \\
 & \Rightarrow \left| B \right|=\dfrac{{{\mu }_{0}}J}{2x}\left[ \dfrac{3{{R}^{2}}}{4} \right] \\
 & \Rightarrow \left| B \right|=\dfrac{3{{\mu }_{0}}J{{R}^{2}}}{8x} \\
\end{align}\]
Therefore the answer has been obtained.

The answer is option D.

Note:
Ampere's Law will permit us to easily calculate the magnetic fields in highly symmetric situations. That is similar to Gauss' Law which allowed us to determine electric fields. Choose the loop such that the magnitude of the magnetic field is fixed and the field is parallel to the loop.