
An infinite, uniformly charged sheet with surface charge density $\sigma $ cuts through a spherical Gaussian surface of radius R at a distance x from its centre, as shown in the figure. The electric flux $\Phi $ through the Gaussian surface is:

$\begin{align}
& \text{A}\text{. }\dfrac{\pi {{R}^{2}}\sigma }{{{\varepsilon }_{0}}} \\
& \text{B}\text{. }\dfrac{2\pi \left( {{R}^{2}}-{{x}^{2}} \right)\sigma }{{{\varepsilon }_{0}}} \\
& \text{C}\text{. }\dfrac{2\pi {{\left( R-x \right)}^{2}}\sigma }{{{\varepsilon }_{0}}} \\
& \text{D}\text{. }\dfrac{\pi \left( {{R}^{2}}-{{x}^{2}} \right)\sigma }{{{\varepsilon }_{0}}} \\
\end{align}$

Answer
591.3k+ views
Hint: Gauss’s law gives the total electric flux through a closed surface containing charges as the charge divided by the permittivity of free space. In this question we have the gaussian surface and the charged sheet. Since, we have the surface charge density, we can find the total charge enclosed by the surface by finding the area of the charged sheet inside the gaussian sphere. Then we can find the total electric flux using Gauss’s law.
Complete answer:
Gauss’s theorem states that the total electric flux through a closed surface is equal to the total charge enclosed by the surface divided by the permittivity of free space.
Electric flux can be defined as the measure of electric field lines passing through a given surface normal to the electric field.
From Gauss’s law, we can mathematically express it as,
$\Phi =\dfrac{Q}{{{\varepsilon }_{0}}}$
Where, $\Phi $ is the electric flux, Q is the total enclosed charge and ${{\varepsilon }_{0}}$ is the permittivity of free space.
In the given question, we will apply the gauss's law to find the electric flux through the given surface.
We need to find the total charge enclosed by the gaussian surface.
Charge density of the sheet is $\sigma $ .
The area of the sheet enclosed by the gaussian surface will be circular. The radius of the circular sheet will be,
$a=\sqrt{{{R}^{2}}-{{x}^{2}}}$
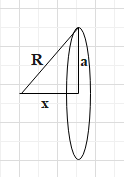
So, the area of the circular sheet inside the gaussian sphere will be,
$A=\pi {{a}^{2}}=\pi \left( {{R}^{2}}-{{x}^{2}} \right)$
The charge enclosed by the gaussian surface is,
$\begin{align}
& Q=\sigma A \\
& Q=\pi \left( {{R}^{2}}-{{x}^{2}} \right)\sigma \\
\end{align}$
So, according to the Gauss’s law, the electric flux through the gaussian surface will be,
$\Phi =\dfrac{Q}{{{\varepsilon }_{0}}}=\dfrac{\pi \left( {{R}^{2}}-{{x}^{2}} \right)\sigma }{{{\varepsilon }_{0}}}$
So, the correct answer is “Option D”.
Note:
Integral form of the Gauss’s law can be given as the area integral of the electric field over any closed surface is equal to the total charge enclosed by the surface divided by the permittivity of free space. We can mathematically express it as,
$\oint{\vec{E}.d\vec{A}=\dfrac{Q}{{{\varepsilon }_{0}}}}$
Complete answer:
Gauss’s theorem states that the total electric flux through a closed surface is equal to the total charge enclosed by the surface divided by the permittivity of free space.
Electric flux can be defined as the measure of electric field lines passing through a given surface normal to the electric field.
From Gauss’s law, we can mathematically express it as,
$\Phi =\dfrac{Q}{{{\varepsilon }_{0}}}$
Where, $\Phi $ is the electric flux, Q is the total enclosed charge and ${{\varepsilon }_{0}}$ is the permittivity of free space.
In the given question, we will apply the gauss's law to find the electric flux through the given surface.
We need to find the total charge enclosed by the gaussian surface.
Charge density of the sheet is $\sigma $ .
The area of the sheet enclosed by the gaussian surface will be circular. The radius of the circular sheet will be,
$a=\sqrt{{{R}^{2}}-{{x}^{2}}}$
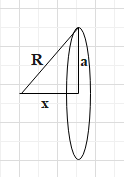
So, the area of the circular sheet inside the gaussian sphere will be,
$A=\pi {{a}^{2}}=\pi \left( {{R}^{2}}-{{x}^{2}} \right)$
The charge enclosed by the gaussian surface is,
$\begin{align}
& Q=\sigma A \\
& Q=\pi \left( {{R}^{2}}-{{x}^{2}} \right)\sigma \\
\end{align}$
So, according to the Gauss’s law, the electric flux through the gaussian surface will be,
$\Phi =\dfrac{Q}{{{\varepsilon }_{0}}}=\dfrac{\pi \left( {{R}^{2}}-{{x}^{2}} \right)\sigma }{{{\varepsilon }_{0}}}$
So, the correct answer is “Option D”.
Note:
Integral form of the Gauss’s law can be given as the area integral of the electric field over any closed surface is equal to the total charge enclosed by the surface divided by the permittivity of free space. We can mathematically express it as,
$\oint{\vec{E}.d\vec{A}=\dfrac{Q}{{{\varepsilon }_{0}}}}$
Recently Updated Pages
Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Business Studies: Engaging Questions & Answers for Success

Trending doubts
Which are the Top 10 Largest Countries of the World?

What are the major means of transport Explain each class 12 social science CBSE

Draw a labelled sketch of the human eye class 12 physics CBSE

Why cannot DNA pass through cell membranes class 12 biology CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

Draw a neat and well labeled diagram of TS of ovary class 12 biology CBSE




