Question

An ideal Carnot engine whose efficiency 40% receives heat at 500K. If the efficiency is to be 50% then the temperature of sink will be
A. 600K
B. 800K
C. 1000K
D. 250K

Answer 1

Hint: Carnot engine is the most efficient engine possible. Efficiency of the engine is the ratio of energy given to output energy. Here we have to find the output energy, i.e. the temperature of the sink. To solve for that, we are given the temperature of source and the efficiency of the engine. Applying the given details in the equation to find the efficiency of the engine we get the temperature of the sink.

Formula Used:
$\eta =1-\dfrac{{{T}_{2}}}{{{T}_{1}}}$

Complete step-by-step answer:
Look at the figure of Carnot engine given below

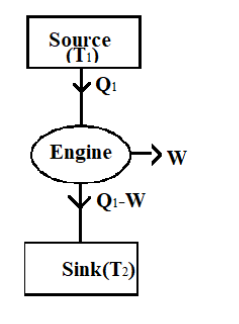
We know that the heat to the engine is provided by the source.
The heat given by the source, \[{{Q}_{1}}\] is given in the question
${{Q}_{1}}=500k$
When the source gives an amount of energy, the Carnot engine does a work W.
Hence the heat that reaches the sink is ${{Q}_{1}}-W$.
In the question we are given the efficiency of the Carnot engine to be 40%.
We know the equation for efficiency of a Carnot engine
$\eta =1-\dfrac{{{T}_{2}}}{{{T}_{1}}}$, where ‘$\eta $’ is the efficiency of the engine, ${{\text{T}}_{\text{2}}}$is the temperature of the sink and ${{\text{T}}_{\text{1}}}$ is the temperature of source.
We know
${{T}_{1}}=500K$ And $\eta =40\%=0.4$
Substituting these values in the equation, we can find the value of ${{\text{T}}_{\text{2}}}$
$\begin{align}
  & \eta =1-\dfrac{{{T}_{2}}}{500} \\
 & 0.4=1-\dfrac{{{T}_{2}}}{500} \\
 & {{T}_{2}}=\left( 1-0.4 \right)\times 500 \\
 & {{T}_{2}}=0.6\times 500 \\
 & {{T}_{2}}=300K \\
\end{align}$
Now we have the temperature of sink when the efficiency of engine is 40% = 300K
We have to find the temperature of the sink when the engine’s efficiency is 50%.
Now we have efficiency ‘$\eta $’ as 50% which is 0.5
Temperature of the source remains the same.
${{T}_{1}}=500K$
To find the temperature of sink,
$\begin{align}
  & \eta =1-\dfrac{{{T}_{2}}}{{{T}_{1}}} \\
 & 0.5=1-\dfrac{{{T}_{2}}}{500} \\
 & {{T}_{2}}=\left( 1-0.5 \right)500 \\
 & {{T}_{2}}=0.5\times 500 \\
 & {{T}_{2}}=250K \\
\end{align}$
Thus we have the temperature of the sink when efficiency of the engine is 50% = 250K.
Hence the correct answer is option D.

Note: Carnot engine is an ideal heat engine that acts on Carnot cycle. The Carnot cycle includes four processes. A reversible isothermal expansion process, a reversible adiabatic expansion, an isothermal reversible compression and an adiabatic reversible compression are the four processes.
It is not possible to have a Carnot engine with 100% efficiency. To attain 100% efficiency the input heat should be completely converted into work; which is not possible.