Question

An emf of 20 V is applied at time t = 0 to a circuit containing in series a 10 mH inductor and 5 \[\Omega \] resistor. The ratio of currents at time \[t=\infty \] and \[t=40s\] is close to: (take \[{{e}^{2}}\]= 7.389 )
A). 1.06
B). 1.46
C). 1.15
D). 0.84

Answer 1

Hint: To solve this question we will be using the equation of current discharge for inductor – resistor circuit. For that, we must know the value of the time constant. So first, we will calculate the time constant and then solve it further. The time constant for the inductor-capacitor circuit is given by inductance over resistance. After calculating the time constant we will substitute its value in the formula for charge-discharge in the circuit and calculate the current at given time intervals.

Formula Used: \[\tau =\dfrac{L}{R}\], where
\[\tau \]= time constant in seconds.
L = inductance in henrys and R = resistance in ohms
\[i={{i}_{0}}(1-{{e}^{-{}^{t}/{}_{\tau }}})\], formula for current discharge.

Complete step-by-step solution:

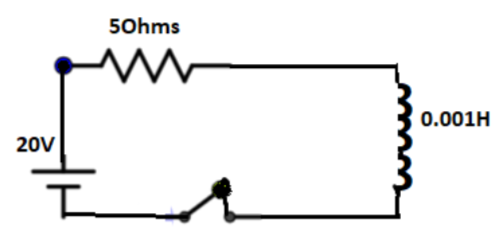
We will first calculate the time constant in seconds
We know,
\[\tau =\dfrac{L}{R}\]
Substitute the given values of L and R
We get,
\[\tau =\dfrac{0.01}{5}\]
\[\tau =0.002\] sec
Now to find the current in the circuit at given time
We know,
\[i={{i}_{0}}(1-{{e}^{-{}^{t}/{}_{\tau }}})\] ……………………………… (A)
After substituting the value of time constant
We get,
\[i={{i}_{0}}(1-{{e}^{-{}^{t}/{}_{0.002}}})\]
Therefore,
\[i={{i}_{0}}(1-{{e}^{-500t}})\]
Now substitute t = 40 in above equation
We get,
\[{{i}_{40}}=\dfrac{20}{5}(1-{{e}^{-500\times 40}})\]
Therefore,
\[{{i}_{40}}=4(1-{{e}^{-20000}})\] ………………………… (1)
Similarly we will calculate the current for time t at infinity using equation (A)
\[{{i}_{\infty }}={{i}_{0}}(1-{{e}^{-\infty }})\]
\[{{i}_{\infty }}=\dfrac{20}{5}(1-0)\]
Therefore,
\[{{i}_{\infty }}=4\] ………………………………… (2)
Taking the ratio of currents
Therefore from (1) and (2)
We get,
\[\dfrac{{{i}_{\infty }}}{{{i}_{40}}}=\dfrac{1}{1-{{e}^{-20000}}}\]
\[\dfrac{{{i}_{\infty }}}{{{i}_{40}}}\cong 1\]
We have calculated the ratio which is approximately equal to 1. So, we must carefully select the answer that is closest to 1.
Therefore, the correct answer is option A.

Note: For a resistor-capacitor circuit, the time constant is taken as the product of resistance in ohms and capacitance in farads. However, for the inductor-capacitor circuit, the time constant is calculated as an inductance in henrys over resistance in ohms. This might confuse students.