Question

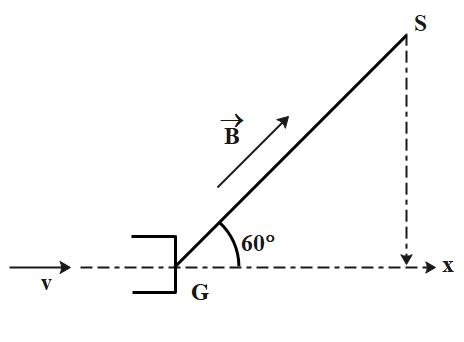
An electron gun G emits electrons of energy 2 keV travelling in the positive x-direction. The electrons are required to hit the spot S where GS = 0.1 m, and the lines GS makes an angle of ${60^ \circ }$ with the x-direction as shown in the figure. A uniform magnetic field B parallel to GS exists in the region outside the electron gun. If the minimum value of B needed to make the electrons hit is ${B_{\min }} = 4.73 \times {10^{ - x}}T$, find x ?

Answer 1

Hint: It is clear from the diagram that the initial velocity makes an arbitrary angle with the direction of the magnetic field, so then the electron will undergo helical motion. Use an expression for kinetic energy to calculate the value of velocity. Afterward, we will form components of the forces acting on the electron and then resolve them accordingly to rearrange the formed equation to give the desired result.

Formula used:
Pitch or the horizontal distance covered by electron, $GS = \dfrac{{2\pi mv\cos \theta }}{{q{B_{\min }}}}$
The kinetic energy of the electron, $E = \dfrac{1}{2}m{v^2}$

Complete step by step answer:
Given:
The energy of electrons, $E = 2keV$
The horizontal distance covered by electron, $GS = 0.1m$
The angle between lines of GS and x-axis, $\theta = {60^ \circ }$
The mass of the electron, $m = 9.1 \times {10^{ - 31}}$Kg
The minimum value of magnetic field intensity, ${B_{\min }} = 4.73 \times {10^{ - x}}T$

Firstly, let’s consider the energy of the electron. As the electron is in motion, so its energy will be completely kinetic energy. If the kinetic energy of the electron is E, and mass of the electron is ‘m and ‘v’ be the velocity of the electron, then the mathematical expression for the same is:
$E = \dfrac{1}{2}m{v^2} \cdots \cdots \cdots \cdots \left( 1 \right)$
Substituting the given values in equation (1), we get:
$\eqalign{
  & E = \dfrac{1}{2}m{v^2} \cr
  & \Rightarrow 2 \times {10^3} \times 1.6 \times {10^{ - 19}} = \dfrac{1}{2} \times 9.1 \times {10^{ - 31}} \times {v^2} \cr
  & \Rightarrow v = \sqrt {\dfrac{{4 \times {{10}^3} \times 1.6 \times {{10}^{ - 19}}}}{{9.1 \times {{10}^{ - 31}}}}} \cr
  & \Rightarrow v = \sqrt 7 \times {10^7} \cr
  & \therefore v = 2.64 \times {10^7}m{s^{ - 1}} \cr} $
Now, if the direction of the magnetic field is not perpendicular to the direction of velocity of the electron, then the electron will undergo helical motion. The velocity component parallel to the magnetic field provides the forward motion while the perpendicular component provides the centripetal force. So here, we just need the parallel component. Pitch or the horizontal distance covered by electron GS is,
$GS = \dfrac{{2\pi mv\cos \theta }}{{q{B_{\min }}}} \cdots \cdots \cdots \cdots \left( 2 \right)$

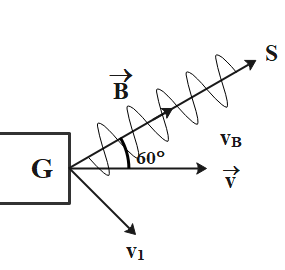
The picture clearly shows that the angle between the magnetic field and velocity is ${60^ \circ }$. So, the minimum magnetic field required will be given by substituting the given and calculated value of velocity in equation (2), so we get:
$\eqalign{
  & GS = \dfrac{{2\pi mv\cos \theta }}{{q{B_{\min }}}} \cr
  & \Rightarrow {B_{\min }} = \dfrac{{2\pi mv\cos \theta }}{{q\left( {GS} \right)}} \cr
  & \Rightarrow {B_{\min }} = \dfrac{{2\pi \times 9.1 \times {{10}^{ - 31}} \times 2.64 \times {{10}^7}\cos {{60}^ \circ }}}{{1.6 \times {{10}^{ - 19}}\left( {0.1} \right)}} \cr
  & \therefore {B_{\min }} = 4.73 \times {10^{ - 3}}T \cr} $
By comparing the given expression for the minimum value of B and the calculated one, we get x is 3.
Therefore the value of x is 3.

Note:
A moving charged particle will experience no force if it is parallel to the magnetic field and thus the charged particle will continue moving along its line of force. But if the initial velocity of the charged particle is perpendicular to the magnetic field, then the force acting on it will be such that it continuously deflects the particle sideways without changing its velocity, thus resulting in a circular motion. These phenomena must be crystal clear to the students to solve problems like the given.