Question

An electron and a proton are moving on straight parallel paths with the same velocity. They enter a semi-infinite region of uniform magnetic field perpendicular to the velocity. Which of the following statement(s) is/are true?
This question has multiple correct options.
A. They will never come out of the magnetic field region.
B. They will come out travelling along parallel paths.
C. They will come out at the same time.
D. They will come out at different times.

Answer 1

Hint: It is said that an electron and a proton moving with same velocity enters a magnetic field. By finding the trajectory of the electron and proton inside the magnetic field we can find if they will leave the field or will never leave the field. By calculating the time taken by the proton and time taken by the electron to leave the field, we can compare whether they are equal or not.
Formula used:
$\text{time=}\dfrac{\text{distance}}{\text{speed}}$

Complete Answer:
In the question we have an electron and a proton moving with the same velocity along a straight parallel path.
It is said that these particles enter a semi – infinite region of uniform magnetic field perpendicular to their velocity.
Consider the figure given below.

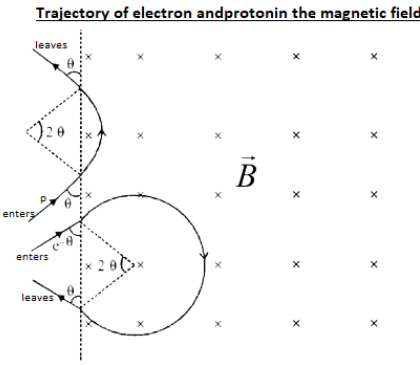
The figure gives us the path of the electron and proton in the magnetic field.
From the figure we can see that both proton and electron enter the magnetic field with the same angle given by ‘\[\theta \]’ and since they have different charges, they deflect in opposite directions within the field. And thus they leave the magnetic fields with the same angle ‘$\theta $’.
Therefore we can say that both electron and proton will come out of the field along parallel paths.
Hence option B is correct A is incorrect.
Now let us consider option C and D. According to option C both the particles come out of the magnetic field at the same time and according to option D both particles come out at different times.
To find which is correct, let us find the time that the particles come out of the field.
We know that time is given as,
$\text{time=}\dfrac{\text{distance}}{\text{speed}}$
$\begin{align}
  & \Rightarrow t=\dfrac{d}{s} \\
 & {\vec{B}} \\
\end{align}$
Therefore the time taken by proton to leave the magnetic field will be,
${{t}_{p}}=\dfrac{{{d}_{p}}}{{{v}_{p}}}$
The distance traveled by the proton in the magnetic field is the length of the arc it made inside the magnetic field.
We know that arc length is the product of angle and radius of the arc.
From the figure, we can see that the angle of the arc made by the proton is ‘$2\theta $’ and let ‘${{r}_{p}}$’ be the radius of the arc and in the question it is said that the velocity of proton and electron is the same, let this be ‘v’.
Thus we get time as,
$\Rightarrow {{t}_{p}}=\dfrac{2\theta \times {{r}_{p}}}{v}$
We know that the radius of the path made by proton,
${{r}_{p}}=\dfrac{{{m}_{p}}v}{eB}$
We can substitute this in the equation of time, thus we get
$\Rightarrow {{t}_{p}}=\dfrac{2\theta }{v}\times \dfrac{{{m}_{p}}v}{eB}$
By simplifying this, we get
$\Rightarrow {{t}_{p}}=\dfrac{2\theta \times {{m}_{p}}}{eB}$
Similarly let us find the time taken by the electron to leave the magnetic field.
This also given as,
${{t}_{e}}=\dfrac{\text{arc length}}{\text{velocity}}$
Here the angle of arc made by the electron is $\left( 2\pi -2\theta \right)$ and radius will be ‘${{r}_{e}}$’.
Therefore we get time as,
$\Rightarrow {{t}_{e}}=\dfrac{\left( 2\pi -2\theta \right){{r}_{e}}}{v}$
Here also we have the radius of the path of the electron,
${{r}_{e}}=\dfrac{{{m}_{e}}v}{eB}$
By substituting this in the equation for time we get time as,
$\Rightarrow {{t}_{e}}=\dfrac{\left( 2\pi -2\theta \right)}{v}\times \dfrac{{{m}_{e}}v}{eB}$
By simplifying this equation,
$\Rightarrow {{t}_{e}}=\dfrac{\left( 2\pi -2\theta \right)\times {{m}_{e}}}{eB}$
Therefore we get time taken by proton to come out as ${{t}_{p}}=\dfrac{2\theta \times {{m}_{p}}}{eB}$ and time taken for the electron to come out of the field as ${{t}_{e}}=\dfrac{\left( 2\pi -2\theta \right)\times {{m}_{e}}}{eB}$.
From this we can see that ${{t}_{p}}\ne {{t}_{e}}$.
Therefore option C is incorrect and D is correct.

Thus the correct answers are option B and D.

Note:
We know that an electron and a proton will have circular paths in a uniform magnetic field; this is because all charged particles will take a circular path in a uniform magnetic field.
The radius of the uniform circular path of a charged particle is given as,
$r=\dfrac{mv}{qB}$, where ‘m’ is mass of the particle, ‘v’ is velocity of the particle, ‘q’ is charge of the particle and ‘B’ is the magnetic field.
In this case we take charge of the particle (q) as ‘e’. This is because we know that charge of an electron is ‘e’ and charge of a proton is the same as the charge of the electron in magnitude.