Question

An automobile is turning around a circular road of radius, $r$. The coefficient of friction between the tyres and the road is $\mu $. Then the velocity of the vehicle should not be more than __________.
A) $\sqrt {\dfrac{{\mu g}}{r}} $
B) $\sqrt {\mu rg} $
C) $\mu rg$
D) $\dfrac{{\mu g}}{r}$

Answer 1

Hint:As the automobile moves along the circular track, a centrifugal force will be pushing it away from the centre of the circle. Also, frictional forces exist between the tyres of the vehicle and the road. For the vehicle to move without slipping, the centrifugal force must be balanced by the frictional force.

Formula used:
-The maximum frictional force existing between a body and a contact surface is given by, $f = \mu N$ where $\mu $ is the coefficient of friction and $N$ is the normal force acting on the body in contact with the surface.
-The centrifugal force acting on a body is given by, ${F_c} = \dfrac{{m{v^2}}}{r}$ where $m$ is the mass of the body, $v$ is the velocity of the body and $r$ is the radius of the circle described by the body.

Complete step by step solution.
Step 1: Describe the key points of the problem at hand and sketch a rough figure.
The problem involves a vehicle undergoing circular motion. The radius of the circular path is mentioned to be $r$. As the automobile moves, it also experiences a frictional force. We have to determine the maximum possible velocity of the car so that it does not slip.
The forces acting on the car will be the centrifugal force ${F_c}$ and the frictional force $f$. We are given $\mu $ as the coefficient of friction existing between the tyres of the vehicle and the road. The figure below is a rough sketch of the motion along the road.

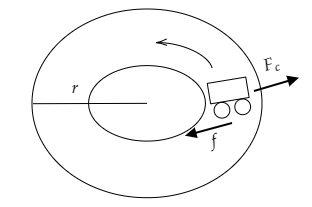
Step 2: Express the condition to be met for the smooth motion of the vehicle around the circular road.
Let $m$ be the mass of the vehicle and its velocity be $v$ .
Then the normal force acting on the automobile will be $N = mg$ ; $g$ is the acceleration due to gravity.
So the maximum frictional force acting between the tyres and the road can be expressed as $f = \mu N = \mu mg$ -------- (1)
The centrifugal force acting on the vehicle can be expressed as ${F_c} = \dfrac{{m{v^2}}}{r}$ -------- (2)
Now for the smooth motion of the vehicle, its centrifugal force must only be equal to or less than the frictional force.
i.e., ${F_c} \leqslant f$ ----------- (3)
Substitute equations (1) and (2) in (3) to obtain $\dfrac{{m{v^2}}}{r} \leqslant \mu mg$
$ \Rightarrow {v^2} \leqslant \mu rg$ .
Then the maximum velocity of the vehicle can be $v \leqslant \sqrt {\mu rg} $ .

So the correct option is B.

Note:Centrifugal force refers to the apparent force felt by the automobile that tries to push it out of its path. It will be directed away from the centre of the circular road. It is the centripetal force that tries to keep the vehicle along the curved road and hence will be directed towards the centre of the rotation. Both the centrifugal force and the centripetal force have the same magnitude but have opposite directions.