Question

An aircraft executes a horizontal loop at a speed of 720 km/h with its wings banked at \[{{15}^{0}}\]. What is the radius of the loop for a safe turn?

Answer 1

Hint: We have to first generalize by drawing a free body diagram representing all the forces acting on the aircraft.The speed is given in km/h which we will change into m/s to find the radius and there is no need to convert the angle into degree radians.

Complete step by step answer:
Speed of aircraft= 720 km/h
Converting it into m/s, \[720\times \dfrac{5}{18}=200m/s\]
Let us take the acceleration due to gravity to be 10 \[m/{{s}^{2}}\]. The angle of banking is \[{{15}^{0}}\] using the formula which we use during the banking of roads where the car takes a turn.

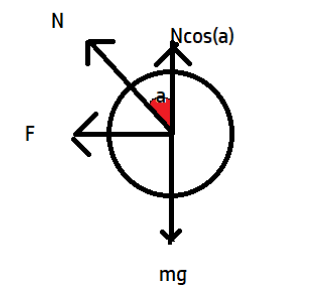
We can see that mg is balanced by cos component of normal force so,
\[\Rightarrow N\cos \theta =mg\]-------(1)
And the centripetal force is balanced by the sine component of normal force,
\[\Rightarrow N\sin \theta =\dfrac{m{{v}^{2}}}{r}\]--(2)
Dividing eq (2) by (1) we get,
\[\begin{align}
&\Rightarrow \tan \theta =\dfrac{{{v}^{2}}}{rg} \\
&\Rightarrow r=\dfrac{{{v}^{2}}}{g\tan \theta } \\
\end{align}\]
Putting the values, we get,
\[\therefore =\dfrac{{{200}^{2}}}{10\times \tan (15)}=\dfrac{400}{0.26}=14.92m\]

So, the radius of the loop is 14.92 m.

Note:Here while resolving the Normal force we have to be careful and since there is no motion in the vertical direction we have equated the two vertical forces, and also the velocity is taken in m/s so that the radius comes out to be in metres in place of kilometres.
Moreover, banking turns are used to change the aircraft heading. The turn is initiated by banking on one side slightly. It is done by lowering one of the ailerons and raising the other aileron.