Question

An aeroplane leaves an airport and flies due north at a speed of $1000$ km per hour. At the same time, another aeroplane leaves the same airport and flies due west at a speed of $1200$ km per hour. How far apart will the two planes be after $1\dfrac{1}{2}$ hours?

Answer 1

Hint: We want to find that at what distance the two planes will be apart from each other.
For that, consider $\Delta ABC$. Find the distance by $\text{Distance=speed}\times \text{time}$. After that use the Pythagoras theorem to find the distance between two planes. Try it and you will get the answer.

Complete step-by-step answer:
We are given the question that speed of north flying aeroplane$=1000$km per hour and speed of west flying aeroplane$=1200$km per hour.

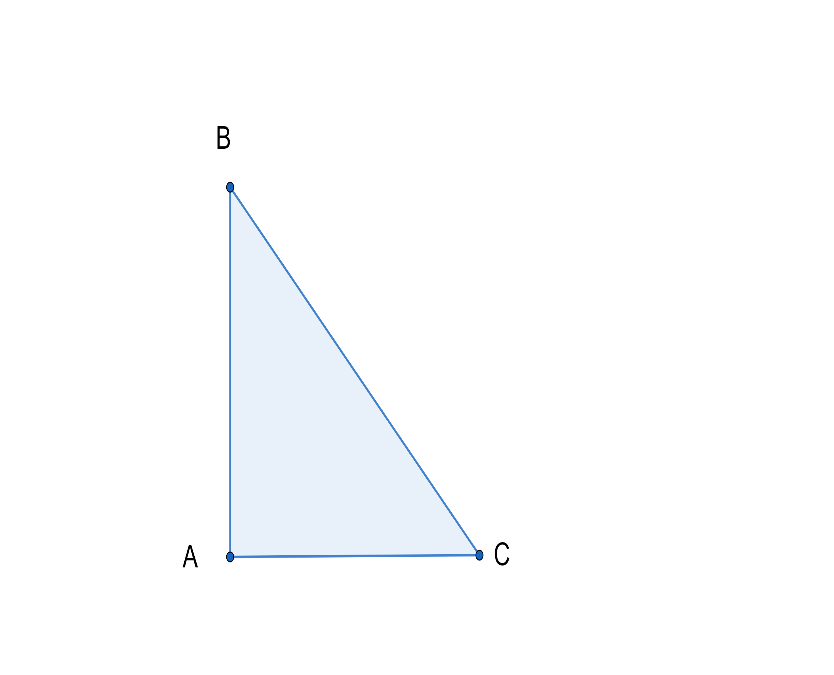
Here we want to find the distance between two planes after $1\dfrac{1}{2}$ hours i.e.$BC$.
The speed of an object is the magnitude of the change of its position; it is thus a scalar quantity. The average speed of an object in an interval of time is the distance travelled by the object divided by the duration of the interval; the instantaneous speed is the limit of the average speed as the duration of the time interval approaches zero.
Speed denotes only how fast an object is moving, whereas velocity describes both how fast and in which direction the object is moving. If a car is said to travel at $60$km per hour, its speed has been specified. However, if the car is said to move at $60$ km per hour to the north, its velocity has now been specified.
The big difference can be discerned when considering movement around a circle. When something moves in a circular path and returns to its starting point, its average velocity is zero, but its average speed is found by dividing the circumference of the circle by the time taken to move around the circle. This is because the average velocity is calculated by considering only the displacement between the starting and endpoints, whereas the average speed considers only the total distance travelled.

We know $\text{speed=}\dfrac{\text{Distance}}{\text{time}}$.
So $\text{Distance=speed}\times \text{time}$.
So for North flying plane speed in $1000$km per hour and time taken is $1\dfrac{1}{2}=\dfrac{3}{2}$hours.
Distance for the north flying plane$=1000\times \dfrac{3}{2}=1500$km.
So for West flying plane speed in $1200$km per hour and time taken is $1\dfrac{1}{2}=\dfrac{3}{2}$hours.
Distance for the west flying plane$=1200\times \dfrac{3}{2}=1800$km.
Now we have to find $BC$.
Since we know north and west are perpendicular,
$\angle BAC=90{}^\circ $
So $\Delta ABC$ is a right-angle triangle.
Now using Pythagoras theorem,
${{(Hypotenuse)}^{2}}={{(Height)}^{2}}+{{(Base)}^{2}}$
Here $AB=(Height)$and$AC={{(Base)}^{2}}$.
$\begin{align}
  & {{(BC)}^{2}}={{(AB)}^{2}}+{{(AC)}^{2}} \\
 & {{(BC)}^{2}}={{(1500)}^{2}}+{{(1800)}^{2}} \\
 & (BC)=3\times 100\times \sqrt{61}=300\sqrt{61} \\
\end{align}$
$(BC)=300\sqrt{61}$km.
So we get that two planes will be $300\sqrt{61}$km apart from each other.

Note: Read the question carefully. Also, you should know the basics such as $\text{speed=}\dfrac{\text{Distance}}{\text{time}}$and ${{(Hypotenuse)}^{2}}={{(Height)}^{2}}+{{(Base)}^{2}}$. Don’t jumble yourself while substituting values. While simplifying do not make silly mistakes such as don’t forget to square it.