Question

An aeroplane flying horizontally with a speed of 360km/h releases a bomb at a height of 490m from the ground. If g= 9.8m/, it will strike the ground at
A) 10km
B) 100km
C) 1km
D) 16km

Answer 1

Hint:To find the distance between two points, firstly find out the time of flight and then multiply the time with velocity in this way we will find the distance from where the aeroplane releases the bomb at the ground.

Complete step by step solution: To understand the solution firstly we draw the diagram

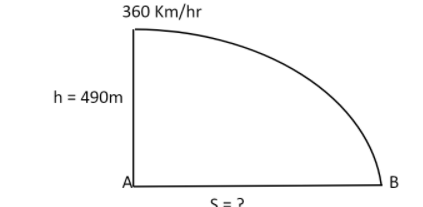
Let us consider two points AB. Here B is that point where the bomb is struck at ground. Consider one more point just above the point A. This is that point where the aeroplane is flying horizontally with a velocity of 360 km/h.

Height from aeroplane to ground = 490m

Horizontal direction velocity is 360km/h and vertical direction initial velocity is zero

In the diagram s is that distance which is covered by the bomb from aeroplane to point B.

To find out the distance firstly we find out the time of flight and this time is multiplied by the
velocity. We know the value of velocity.
\[v = 360km/h\]

Always remember that in the horizontal direction velocity is constant. Then we know that:
\[S = t*v\] (i)

We know that,
$h = ut + \dfrac{1}{2}a{t^2}$
Here, h is vertical height

u is vertical initial velocity
a is acceleration due to gravity downward
t is time
u is zero because vertical velocity is zero
$a = 9.8m/{s^2}$

After putting all these values we get
$\begin{gathered}
h = \dfrac{1}{2}a{t^2} \\
t = \sqrt {\dfrac{{2h}}{a}} \\
\end{gathered} $

Put the value of h and a, we get the value t
\[\begin{array}{*{20}{l}}
{t = \sqrt {\dfrac{{2 \times 490}}{{9.8}}} } \\
{t = \sqrt {100} } \\
{t = 10{\text{ }}sec}
\end{array}\]

Put the value of t and v, we get the distance
\[\begin{array}{*{20}{l}}
{S = t*v} \\
{t = 10{\text{ }}sec}
\end{array}\]

Time is in sec. First of all, convert it into hours, we get
\[\begin{array}{*{20}{l}}
{t = \dfrac{{10}}{{3600}}} \\
{s{\text{ = }}\left( {\dfrac{{10}}{{3600}}} \right)*360} \\
{s = 1km}
\end{array}\]


Hence, the correct answer is Option C.

Note:When an aeroplane releases a bomb, the bomb usually follows a parabolic trajectory assuming that its horizontal speed is equal to that of the airplane. We can say that the projectile motion is a motion that is experienced by a particle being projected near the surface of earth and which moves along a curved path under the gravitational force.