An aeroplane flying at a height of 300 meters above the ground passes vertically above another plane at an instant when the angles of elevation of the two planes from the same point on the ground are 60 degrees and 45 degrees respectively. Then the height of the lower plane from the ground in meters is:
(a). $100\sqrt{3}$
(b). $\dfrac{100}{\sqrt{3}}$
(c). 50
(d). $150\left( \sqrt{3}+1 \right)$
Answer
Verified359.4k+ views
Hint: At first try to draw the picture according to the conditions. From the picture point out what you have to find out and which values are given to you. Then apply trigonometric ratios accordingly.
Complete step-by-step answer:
Let A be aeroplane flying at a height of 300 meters above the ground.
It passes vertically above another plane, say B.
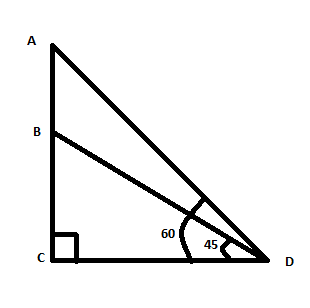
Let $CD$ be the ground.
It is given that the height of the first plane is 300 meters.
That means $AC$ is the height which is 300 meters.
It is given that the angle of the elevation of the two planes from the same point on the ground are 60 and 45 degrees respectively.
The angle of elevation is an angle that is formed between the horizontal line and the line of sight. If the line of sight is upward from the horizontal line, then the angle formed is an angle of elevation.
Here the objects are the aeroplane. D is the observation point. The horizontal line is $CD$.
$\begin{align}
& \angle ADC={{60}^{\circ }} \\
& \angle BDC={{45}^{\circ }} \\
\end{align}$
Now we have to find out the height of the lower plane from the ground. That means we have to find out $CB$.
From triangle $ACD$ we have:
$\begin{align}
& \tan {{60}^{\circ }}=\dfrac{AC}{CD} \\
& \Rightarrow \sqrt{3}=\dfrac{300}{CD} \\
& \Rightarrow CD=\dfrac{300}{\sqrt{3}} \\
\end{align}$
From triangle $BCD$ we have:
$\begin{align}
& \tan {{45}^{\circ }}=\dfrac{BC}{CD} \\
& \Rightarrow 1=\dfrac{BC}{CD} \\
& \Rightarrow BC=CD=\dfrac{300}{\sqrt{3}}=\dfrac{3\times 100}{\sqrt{3}}=\dfrac{{{\left( \sqrt{3} \right)}^{2}}\times 100}{\sqrt{3}}=100\sqrt{3} \\
\end{align}$
The height of the lower plane from the ground is $100\sqrt{3}$ meters.
Hence, option (a) is correct.
Note: Since we have to find out the height here and in both the triangles the base is the same, try to use the height and base ratio. If we go for height and hypotenuse ratio it will become more lengthy.
Complete step-by-step answer:
Let A be aeroplane flying at a height of 300 meters above the ground.
It passes vertically above another plane, say B.
Let $CD$ be the ground.
It is given that the height of the first plane is 300 meters.
That means $AC$ is the height which is 300 meters.
It is given that the angle of the elevation of the two planes from the same point on the ground are 60 and 45 degrees respectively.
The angle of elevation is an angle that is formed between the horizontal line and the line of sight. If the line of sight is upward from the horizontal line, then the angle formed is an angle of elevation.
Here the objects are the aeroplane. D is the observation point. The horizontal line is $CD$.
$\begin{align}
& \angle ADC={{60}^{\circ }} \\
& \angle BDC={{45}^{\circ }} \\
\end{align}$
Now we have to find out the height of the lower plane from the ground. That means we have to find out $CB$.
From triangle $ACD$ we have:
$\begin{align}
& \tan {{60}^{\circ }}=\dfrac{AC}{CD} \\
& \Rightarrow \sqrt{3}=\dfrac{300}{CD} \\
& \Rightarrow CD=\dfrac{300}{\sqrt{3}} \\
\end{align}$
From triangle $BCD$ we have:
$\begin{align}
& \tan {{45}^{\circ }}=\dfrac{BC}{CD} \\
& \Rightarrow 1=\dfrac{BC}{CD} \\
& \Rightarrow BC=CD=\dfrac{300}{\sqrt{3}}=\dfrac{3\times 100}{\sqrt{3}}=\dfrac{{{\left( \sqrt{3} \right)}^{2}}\times 100}{\sqrt{3}}=100\sqrt{3} \\
\end{align}$
The height of the lower plane from the ground is $100\sqrt{3}$ meters.
Hence, option (a) is correct.
Note: Since we have to find out the height here and in both the triangles the base is the same, try to use the height and base ratio. If we go for height and hypotenuse ratio it will become more lengthy.
Last updated date: 19th Sep 2023
•
Total views: 359.4k
•
Views today: 6.59k
