Question

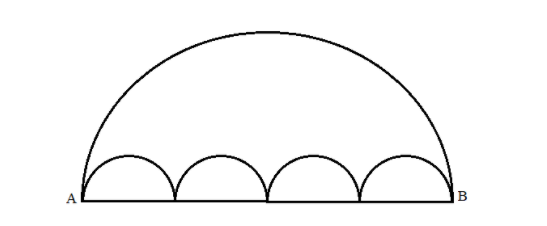
All the arcs in the following diagram are semi-circles. This diagram shows two paths connecting A to B. Path \[1\] is the single large semi-circle and path \[2\] consists of the chain of small semi-circles. Then

A. Path \[1\] is longer than path \[2\]
B. Path \[1\] is of the same length as path \[2\]
C. Path \[1\] is shorter than path \[2\]
D. Path \[1\] is of the same length as path \[2\] , only if the number of semi-circles is not more than \[4\] .

Answer 1

Hint: Some of the thing we need to know before solving this question:
Half of the circle is known as a semi-circle. Therefore, the area of the semi-circle will be half of the area of the circle.
Area of a circle is \[\pi {r^2}\] then, area of a semicircle is \[\dfrac{{\pi {r^2}}}{2}\] where \[r\] is the radius of circle or radius of semi-circle. Perimeter of a semicircle is given by, \[\pi r + 2r\] where \[r\] is the radius of the semi-circle.

Complete step by step answer:
The given diagram consists of one large semi-circle and four small semi-circles. Thus, we have two paths to reach B from A.
It is given that the path \[1\] from A to B is the large semi-circle that is the arc length of that semi-circle. That is the perimeter of a semi-circle minus its diameter, since this path doesn’t include the diameter. And it is given by \[\pi r + 2r - d\] where \[r\] is the radius of the semi-circle and \[d\] is the diameter of the semi-circle.
We know that diameter is nothing but twice the radius that is, \[d = 2r\] . Thus, we get, \[\pi r + 2r + 2r\] .
On simplifying this we get, \[\pi r\] . Thus, Path \[1 = \] \[\pi r\] .
Let’s calculate the path \[2\] . It is given that path \[2\] is the way along the small four semi-circles. That is nothing but the perimeter of those four semicircles minus their diameters, since the path doesn’t cover its diameters. Since all four semi-circles are equal, we get, \[4 \times (\pi r)\] . Thus, Path \[2 = \] \[4\pi r\] .
On comparing both parts we get, Path \[1 < \] Path \[2\] . Since, \[\pi r < 4\pi \] is obvious.
Therefore, Path \[1\] is smaller than Path \[2\] .
Let us see the options, option (a) Path \[1\] is longer than path \[2\] this cannot be a correct answer since Path \[1\] is smaller than Path \[2\] .
Option (b) Path \[1\] is of the same length as path \[2\] , also this cannot be the correct answer since Path \[1\] is smaller than Path \[2\] .
Option (c) Path \[1\] is shorter than path \[2\] , this is the correct answer since Path \[1\] is smaller than Path \[2\] .
Option (d) Path \[1\] is of the same length as path \[2\] , only if the number of semi-circles is not more than \[4\] , this cannot be the correct answer since Path \[1\] is smaller than Path \[2\] .

So, the correct answer is “Option C”.

Note: Since the path is from A to B, we cannot walk through the diameter of the semicircle clearly, they said that we need to walk through the arc. Thus, the path is the perimeter of the semi-circle except the diameter thus we neglected the diameter from the formula. Same idea is applied for those four semicircles.