Question

$A=\left\{ x:x\ is\ a\ perfect\ square,\ x<50,x\in N \right\}$
$B=\left\{ x:x=8m+1,\ where\ m\in W,\ s<50,x\in N \right\}$, then find $A\cap B$ and display it with a Venn diagram.

Answer 1

Hint: Write down all the elements of sets A and B by using the information given in words. $A\cap B$represents the common elements in sets A and B.

Complete step-by-step answer:
Here, sets A and B defined as
$A=\left\{ x:x\ is\ a\ perfect\ square,\ x<50,x\in N \right\}$
and
$B=\left\{ x:x=8m+1,\ where\ m\in W,\ s<50,x\in N \right\}$
Now, let us represent A and B in set – builder form.
As A has perfect square numbers which should be less than 50. Hence, we can write elements of A as;
$A=\left\{ 1,4,9,16,25,36,49 \right\}...........\left( 1 \right)$
Now, elements of B are defined as $x=8m+1$, where m is a whole number with condition that x should be less than 50.
Now, let us put $m=0,1,2,3........$ to get values of x i.e. elements of B.
As, $x=8m+1$ where $m=0,1,2,3........$
$\begin{align}
  & x=8\left( 0 \right)+1=1 \\
 & x=8\left( 1 \right)+1=8 \\
 & x=8\left( 2 \right)+1=17 \\
 & x=8\left( 3 \right)+1=25 \\
 & x=8\left( 4 \right)+1=33 \\
 & x=8\left( 5 \right)+1=41 \\
 & x=8\left( 6 \right)+1=49 \\
 & x=8\left( 7 \right)+1=57 \\
\end{align}$
Which is higher than 50. Hence, elements of B can be given as;
$B=\left\{ 1,8,17,25,33,41,49 \right\}............\left( 2 \right)$
Now, we have to calculate $A\cap B$which means elements common to both A and B.
Hence, $A\cap B$can be written as;
$A\cap B=\left\{ 1,25,49 \right\}$
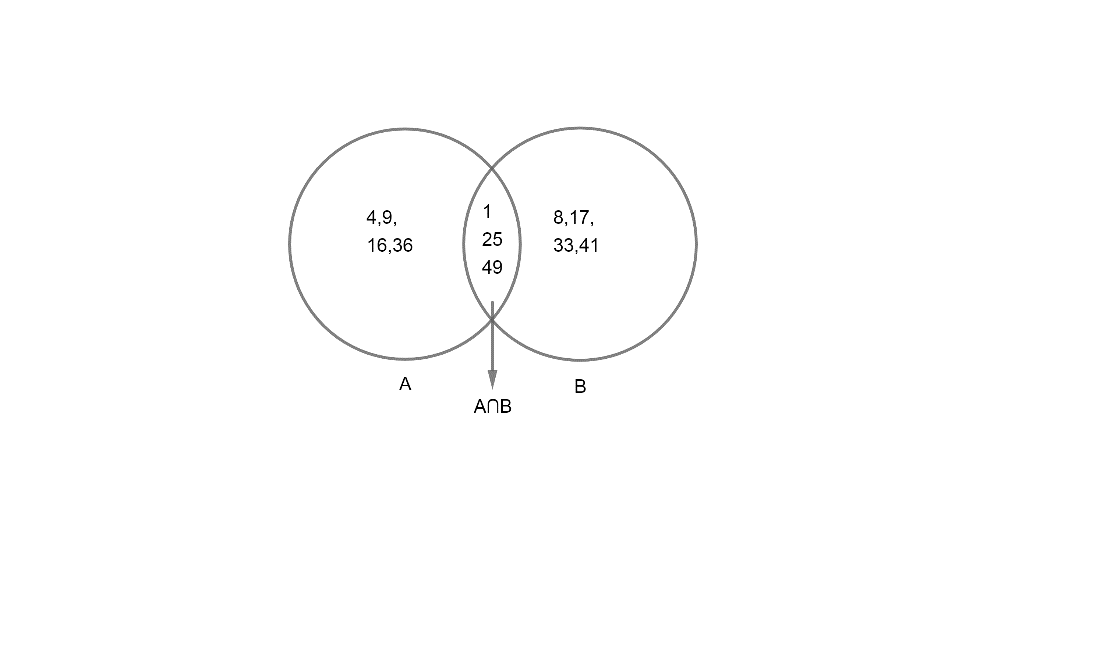
Now, let us represent the given sets by Venn diagram. Venn diagram means defining elements of the given sets with graphical representation.
We have,
$A=\left\{ 1,4,9,16,25,36,49 \right\}$
$B=\left\{ 1,8,17,25,33,41,49 \right\}$
$A\cap B=\left\{ 1,25,49 \right\}$
Hence, Venn diagram is given as;

Note: One can go wrong while writing the elements of A and B. One can miss some elements or write down more elements to A and B without taking care of x <50 or s <50.
One can make mistakes with the second set B where he/she misses the condition $m\in W$ i.e. the whole number and can start writing elements from m = 1 and forget about m = 0. Hence, be careful with these kinds of questions where $x\in W,x\in N\ or\ x\in Z$ plays an important role.
One can miss some elements of ‘$A\cap B$’ while representing the Venn diagram. Hence, be careful with the display of Venn diagrams.