Question

\[ABCD\;\]is a trapezium with \[AB\parallel DC\]. A line parallel to \[AC\] intersects \[AB\] at \[X\] and \[BC\] at \[Y\].
Prove that \[ar(\Delta ADX) = ar(\Delta ACY)\].

Answer 1

Hint – In the figure join \[YA,XC,XD\] then use the concept of area of triangle.

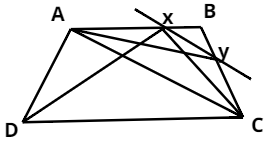
\[ABCD\] is a trapezium with \[AB\parallel DC\;,\;XY\parallel AC\].
Join \[YA,XC,XD\].
Triangles \[ACX\] and \[ACY\] have the same base \[AC\] and are between parallel lines \[AC\;\] and \[XY\].
$ar(\Delta ACX) = ar(\Delta ACY)\,\,\,\,\,\,......(i)$
We know , two triangles with the same base and vertex of both triangles on a line which is parallel to base are in the same area .
Triangles \[ACX\] and \[ADX\] have the same base \[AX\] and are between parallel lines \[AB\] and \[DC\].
So, \[ar(\Delta ACX) = ar(\Delta ADX)\;......\left( {ii} \right)\]
From $(i)$ and $(ii)$ we get,
\[ar(\Delta ADX) = ar(\Delta ACY)\;\]
Hence proved.

Note – In these types of questions we must have to draw diagrams. Since with the help of diagrams only we can do this question . For that we have to know about trapezium (A quadrilateral with one pair of sides parallel) We have to know the concept that two triangles with the same base and vertex of both triangles on the line which is parallel to base are same in area.