Question

ABCD is a rhombus with $\angle ABC=56^{\circ}$, then $\angle ACB$ will be:
$\left(a\right)56^{\circ}$
$\left(b\right)124^{\circ}$
$\left(c\right)62^{\circ}$
$\left(d\right)34^{\circ}$

Answer 1

Hint: We are given one angle of the rhombus and we are required to find an angle that is embedded inside the rhombus. For this, we need to be aware about the angle sum properties of rhombus. And also, some other properties because we are not required to find the adjacent angle but an angle which is created by adding an additional line segment, which is the diagonal in this case, inside the rhombus.

Complete step by step answer:
We have the following type of situation:

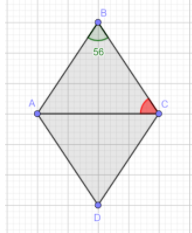
We are given the angle shaded in green and we are required to find the angle shaded in red.
We will first find the $\angle BCD$. To find this angle we will use the property that the consecutive angles of a rhombus are supplementary. So, we have:
$\angle ABC+\angle BCD=180^{\circ}$
Plugging in the value of $\angle ABC$, we have:
$\angle BCD+56^{\circ}=180^{\circ}$
$\implies \angle BCD=124^{\circ}$
Now, we will use the property that the diagonals of a rhombus bisect its interior angles. So, we can say that the following holds true:
$\angle ACB=\dfrac{1}{2}\angle BCD$
Putting the value of the $\angle BCD$ we found earlier, we have:
$\angle ACB=\dfrac{1}{2}\times 124^{\circ}$
$\implies \angle ACB=62^{\circ}$

So, the correct answer is “Option c”.

Note: It is quite common to just simply subtract the given angle from $180^{\circ}$ and then tick the correct answer which would lead to an incorrect answer. So, always check what angle you have been asked to find out. Only after that, use the properties which will help you find the angle.