Question

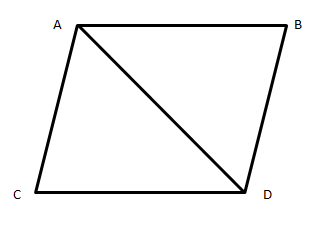
ABCD is a rhombus such that one of its diagonals is equal to its side. Find the number of the angles of rhombus ABCD.
(A) ${45^0},{135^0},{45^0},{135^0}$
(B)${100^0},{80^0},{100^0},{80^0}$
(C)${120^0},{60^0},{120^0},{60^0}$
(D)${60^0},{60^0},{60^0},{60^0}$

Answer 1

Hint- In order to solve this question, we will use the properties of triangles such as the sum of internal angles of a triangle is 180 degree. First we will split the rhombus into two triangles and use the conditions given in the question to solve the question.

Complete step-by-step solution -
Given that one side of rhombus is equal to its diagonal and we know that all sides of rhombus are equal.
Therefore, the triangles formed in the rhombus with common one side common (diagonal ) will be equilateral triangle
So, in $\Delta ABC$ all sides are equal.
Let x be the measure of angles in $\Delta ABD$
$ \Rightarrow x + x + x = {180^0}$ sum of angles in a triangle is ${180^0}$
\[
   \Rightarrow 3x = {180^0} \\
  \therefore x = {60^0} \\
  \therefore \angle B = {60^0} \\
 \]
Now in $\Delta ACD$
Let x be the measure of angles in $\Delta ACD$
$ \Rightarrow x + x + x = {180^0}$
\[
   \Rightarrow 3x = {180^0} \\
  \therefore x = {60^0} \\
  \therefore \angle D = {60^0} \\
 \]
Therefore the angles of the rhombus are
$
   \Rightarrow \angle A = {60^0} + {60^0} = {120^0} \\
   \Rightarrow \angle C = {60^0} + {60^0} = {120^0} \\
 $
Therefore, the angles of the rhombus ABCD are ${120^0},{60^0},{120^0},{60^0}$
Hence the correct option is “C”.

Note- To solve these types of questions remember the basic properties of the rhombus and triangle such as the sum of internal angles of the triangle is 180 degree and the sum of internal angles of a rhombus is 360 degree. All sides of rhombus are equal and the diagonal bisects the angles of rhombus. When all sides of triangles are equal then, then all angles of the triangle are also equal and that triangle is known as an equilateral triangle.