Question

ABCD is a rhombus and ABDE is a parallelogram.
Given that EDC is a straight line and ∠AED = ${36^0}$ , find ∠BAD.

$
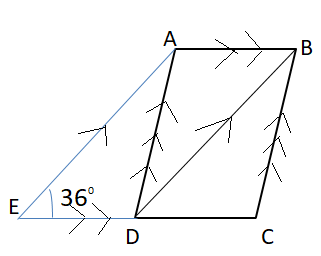
  \left( {\text{a}} \right){\text{ 3}}{{\text{6}}^0} \\
  \left( {\text{b}} \right){\text{ 7}}{{\text{2}}^0} \\
  \left( {\text{c}} \right){\text{ 10}}{{\text{8}}^0} \\
  \left( {\text{d}} \right){\text{ 12}}{{\text{0}}^0} \\
\ $

Answer 1

HINT- In order to solve such types of questions the key concept is that we should know the basic properties of rhombus and parallelogram along with the proper understanding of corresponding angles and alternate angles.

Complete step-by-step answer:
Corresponding angles - When two parallel lines (AE and BD) are crossed by another line EC (which is called the Transversal), the angles (∠BDC = ∠AED) in matching corners are called corresponding angles.

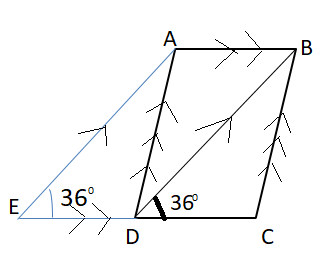
⇒ ∠BDC = ∠AED = ${36^0}$ (corresponding angles of AE and BD.)

⇒ We know that ABCD is a rhombus, so AB∥DC

Alternate angles-
Alternate angles are angles that are in opposite positions relative to a transversal (BD) intersecting two parallel lines (AB and DC).

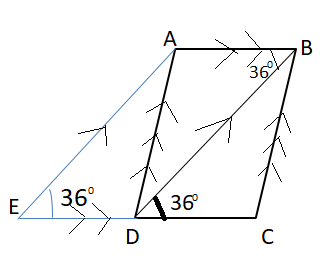
⇒ ∠ABD = ∠BDC = ${36^0}$ (Alternate angles)

Isosceles triangle- The Isosceles Triangle Theorem states: If two sides of a triangle are equal, then the angles opposite those sides are equal.

⇒ ∠ADB = ∠ABD = ${36^0}$ (Base angles of isosceles, since AB =DC)

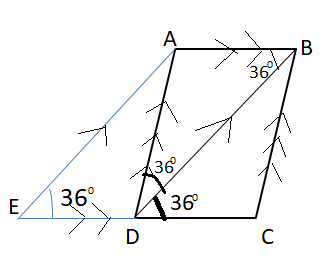
⇒ In △ADB,
Using formula $\left( {{\text{n - 2}}} \right) \times {180^0}$ , Here, number of side n=3
So sum of internal angle of triangle is ${180^0}$
 ⇒ ∠BAD + ∠ABD + ∠ADB = ${180^0}$

Substituting all the values we get,

⇒ ∠BAD + ${36^0}$ + ${36^0}$= ${180^0}$

⇒ ∠BAD = ${180^0}$- ${36^0}$- ${36^0}$
∴ ∠BAD = ${108^0}$
Hence option C is correct.

Note- In Order to solve such types of questions we should know that in a rhombus, opposite sides are parallel and opposite angles are equal. Moreover, all the sides of a rhombus are equal in length while a parallelogram is a quadrilateral with two pairs of parallel sides. The opposite sides of a parallelogram are equal in length and the opposite angles are equal in measure