Question

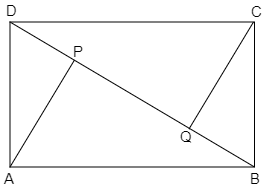
ABCD is a parallelogram and AP and CQ are pedicular from vertices A and C on diagonal BD. Show that $AP = CQ$.

Answer 1

Hint: We will first start by using the fact that if two triangles are congruent then their corresponding parts are equal for proving two triangles congruent. We will use AAS congruence wherein we have to prove two angles and one side are equal.

Complete step by step solution:
Now, we have been given a parallelogram and AP and CQ are perpendicular drawn from vertices A and C and diagonal BD and we have to show that \[AP = CQ\].
Now, we know that the opposite sides of a parallelogram are parallel and equal. Therefore, we have,
$ \Rightarrow AD = BC$.................….. (1)
Also, we have $AD\parallel BC$ and we know that alternate interior angles formed by a transversal cutting a pair of parallel lines are equal. Therefore, we have,
$ \Rightarrow \angle ADB = \angle CBD$...............….. (2)
Now, we know that the angle formed by a straight line is $180^\circ $. Then, we have,
$ \Rightarrow \angle DPA = 90^\circ $
Similarly,
$ \Rightarrow \angle CQB = 90^\circ $
So, it implies that,
$ \Rightarrow \angle DPA = \angle CQB$...............….. (3)
Now, check whether $\Delta DPA$ and $\Delta BQC$ are congruent or not,
$ \Rightarrow \angle DPA = \angle BQC$ (from (3))
$ \Rightarrow AD = BC$ (from (1))
$ \Rightarrow \angle ADB = \angle CBD$ (from (2))
So, by ASA congruence,
$\Delta DPA \cong \Delta BQC$
Now, we know that by the corresponding part of the congruent triangle we have,
$\therefore AP = CQ$
Hence, proved.

Note: In these types of questions, we need to understand what sides and angles of the triangles are given to be equal and what can be proved. Finally, we need to use one of the congruence criteria(ASA, SAS, RHS, SSS, etc.) to prove that the triangles are congruent. Also, we need to understand what each of the congruence criteria means. Like in SAS, the angle should be the included angle between the two sides. Many students do not know this and hence arrive at incorrect results.