Question

ABCD is a cyclic quadrilateral. Find all the angles of this quadrilateral.

Answer 1

Hint: We are given angles of a cyclic quadrilateral in variables. So, we should know some basic properties of the angles of a cyclic quadrilateral. We should know that the opposite angles of a cyclic quadrilateral sum up to $180^{\circ}$. So, using that property we will construct equations and then find the answer.

Complete step by step answer:
A cyclic quadrilateral is a quadrilateral which has all its four vertices lying on a circle. It is also sometimes called inscribed quadrilateral. The circle which consists of all the vertices of any polygon on its circumference is known as the circum-circle or circumscribed circle.
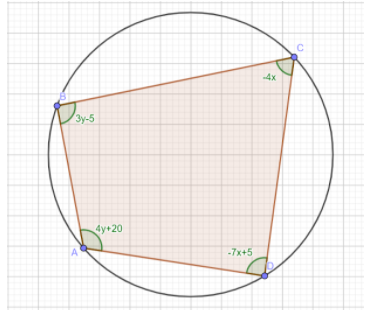
The opposite angles of a cyclic quadrilateral sum up to $180^{\circ}$. So, after looking at the figure we can say that:
$3y-5+\left(-7x+5\right)=180$
$\implies -7x+3y=180$.........$\left(1\right)$
And
$4y+20+\left(-4x\right)=180$
$\implies -4x+4y=160$
$\implies -x+y=40$
$\implies y=x+40$
Putting in $\left(1\right)$
$-7x+3\left(x+40\right)=180$
$\implies -7x+3x+120=180$
$\implies -4x=60$
$\implies x=-15$
Then since $y=x+40$, we have:
$y=40-15=25$
Now, we find all the angles one by one:
$\angle A=4y+20=4\times 25+20=120^{\circ}$
$\angle B=3y-5=3\times 25-5=70^{\circ}$
$\angle C=-4x=-4\times -15=60^{\circ}$
$\angle D=-7x+5=-7\times -15+5=110^{\circ}$
Hence, all the angles have been found.

Note: You can also do the same by finding any two of the adjacent angles and then subtracting that from $180^{\circ}$. For example, say you have found the angle A to be $120^{\circ}$, then there is no need to put the value of $x$ and $y$ to find the value of the opposite angle C. You can simply subtract 120 from 180 and obtain $60^{\circ}$ as the measure of the angle C.