Question

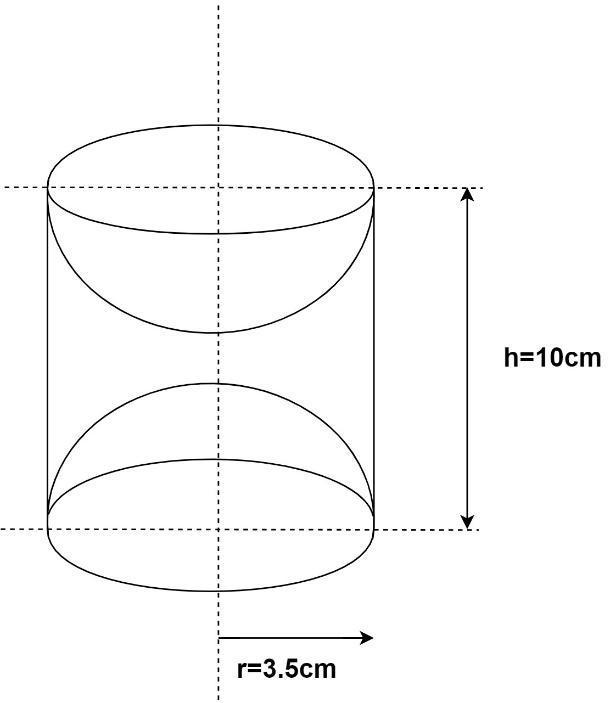
A wooden article was made by scooping out a hemisphere from each end of a solid cylinder. If the height of the cylinder is $10cm$ ,and its base is of radius $3.5cm$ , find the total surface area of the article.
 

Answer 1

Hint: According to the diagram the wooden article is made of a solid cylinder with a hemi-spherical cavity on both ends. so for solving this problem we use the formulas of curved surface area of cylinder and hemisphere.
Given the radius of base of cylinder is $r = 3.5cm$
And height of the cylinder is $h = 10cm$
From the figure above, it is clear that the total surface area of the wooden article is given by
TSA $ = $ Curved surface area of the cylinder$ + 2 \times $ Curved surface area of hemisphere
Curved surface area of cylinder
$
   = 2\pi rh = 2 \times 3.1415 \times 3.5 \times 10 \\
   = 219.911c{m^2} \\
$
We know that curved surface area of a sphere $ = 4\pi {r^2}$
Therefore, curved surface area of hemisphere
\[ = \dfrac{1}{2} \times \] Curved surface area of a sphere.
\[ = \dfrac{1}{2} \times 4\pi {r^2} = 2\pi {r^2} = 2 \times 3.1415 \times 3.5 \times 3.5 = 76.96c{m^2}\]
Therefore, TSA $ = 219.911 + 2 \times 76.96 = 373.84c{m^2}$
Hence the Total Surface area of the article is $373.84c{m^2} \cong 374c{m^2}$.
Note: In these types of questions always remember the formula of curved surface area of the geometrical solids involved. Also try to visualise the sold in order to get a better understanding of the area asked in the problem. Always specify the units along with the answer.