Question

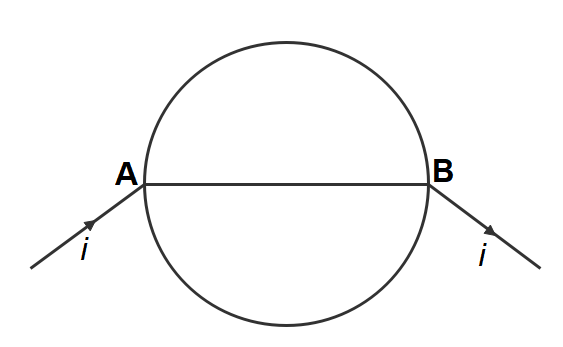
A wire of resistance $0.5\Omega /m$ is bent into a circle of radius 1m. The same wire is connected across a diameter AB as shown in figure. The equivalent resistance is

A. $\pi \,\,ohm$
B. $\left( {\pi + 2} \right)\,\,ohm$
C. $\pi /\left( {\pi + 4} \right)\,\,ohm$
D. $\left( {\pi + 1} \right)\,\,ohm$

Answer 1

Hint: We’re given wire of uniform resistance per unit length. To find the equivalent resistance of the wire, we must approach the problem by finding the resistance of each wire branching from A to B. Once we have the resistances of each wire, we can find the equivalent by considering them as wires connected in parallel.

Formula used:
$\eqalign{
  & {R_C} = 0.5\Omega /m \times 2\pi R \cr
  & \dfrac{1}{{{R_{total}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + \dfrac{1}{{{R_1}}} \cr} $

Complete step-by-step answer:
In the question, they’ve given us a wire of resistance $0.5\Omega /m$. If this wire were to be bent into a circle of radius 1m. The resistance of the circle would be
$\eqalign{
  & {R_C} = 0.5\Omega /m \times length \cr
  & \Rightarrow {R_C} = 0.5\Omega /m \times 2\pi R \cr
  & \Rightarrow {R_C} = 0.5\Omega /m \times 2\pi \times 1m \cr
  & \Rightarrow {R_C} = \pi \Omega \cr} $
Now, another wire is connected across the diameter of the wire, i.e. of length $2R = 2 \times 1m = 2m$. The resistance of this wire will be given by
$\eqalign{
  & {R_2} = 0.5\Omega /m \times 2m \cr
  & {R_2} = 1\Omega \cr} $
Here, you should understand that the wire bent into a circle is divided into two resistance, once the $R_2$ is joined. So, the resistance of the circular part will be two resistors, each of resistance
${R_1} = \dfrac{{{R_C}}}{2} = \dfrac{{\pi \Omega }}{2} = 0.5\pi \Omega $
The connection when normalized into an equivalent electric circuit would look something like this

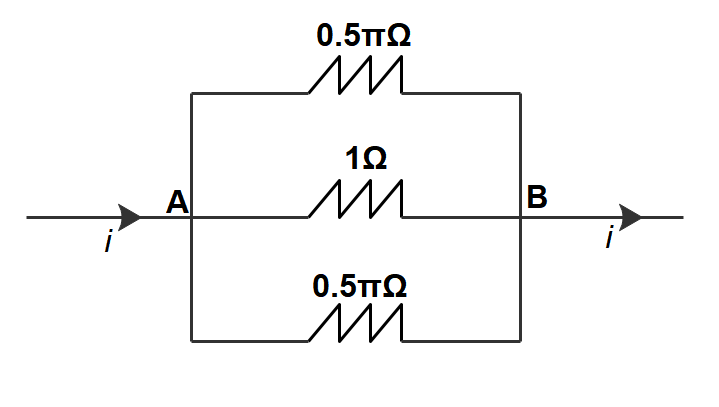
We can clearly see that they’re connected in parallel, across AB. The equivalent resistance will be given by
$\eqalign{
  & \dfrac{1}{{{R_{total}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + \dfrac{1}{{{R_1}}} \cr
  & \Rightarrow {R_{total}} = \dfrac{{{R_1}^2{R_2}}}{{2{R_1}{R_2} + {R_1}^2}} \cr
  & \Rightarrow {R_{total}} = \dfrac{{{{\left( {0.5\pi } \right)}^2} \times 1}}{{\left( {2 \times 0.5\pi \times 1} \right) + {{\left( {0.5\pi } \right)}^2}}} \cr
  & \Rightarrow {R_{total}} = \dfrac{{\dfrac{\pi }{2}}}{{2 + \dfrac{\pi }{2}}} \cr
  & \Rightarrow {R_{total}} = \dfrac{\pi }{{\left( {\pi + 4} \right)}}\Omega \cr} $
Therefore, the equivalent resistance of the circuit will be $\dfrac{\pi }{{\left( {\pi + 4} \right)}}\Omega $.

So, the correct answer is “Option C”.

Note: If you’re wondering how resistances are connected in parallel, you will be able to understand it if you look at junction A. Here, the current ‘i’ will be divided into three parts, as three branches are starting at junction A. You can also find the individual resistances by multiplying each wire’s length with resistance per unit length.