Question

A window of a house is $h$ meter above the ground. From the window, the angles of elevation and depression of the top and bottom of another house situated on the opposite side of the lane are found to be $\alpha $ and $\beta $ respectively. Prove that the height of the house is $h\left( {1 + \tan \alpha \tan \beta } \right)$ meters.

Answer 1

Hint:Draw the diagram as per the given data.Now apply the basic trigonometric formulae and correlate the heights of two different houses.


Complete step-by-step answer:
Firstly, let us note down the given data.
The window is situated at a height of $h$ meters from the ground.
From the window, the angles of elevation and depression of the top and bottom of another house situated on the opposite side of the lane are found to be $\alpha $ and $\beta $ respectively.
Let us assume the height of the house is $H$ meters.
Now we need to prove that $H = h\left( {1 + \tan \alpha \tan \beta } \right)$.
According to the given data, we will get the diagram as follows:

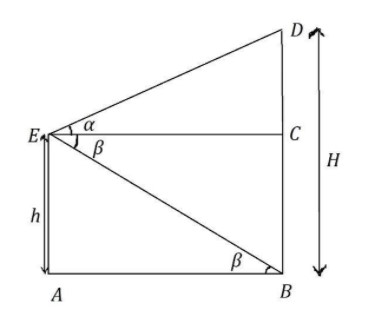
We will find out the length of $EC$ in terms of $H$ and the length of $AB$ in terms of $h$.
And from the diagram, we can conclude that the length of $EC$ and the length of $AB$ will be equal.
So, when we equate those two equations, we will get the value of $H$ in terms of \[h\].
We are going to use some basic formula of trigonometry and that is
$\tan \alpha = \dfrac{{{\text{Opposite}}}}{{Adjacent}}$. We are going to apply this formula in the coming steps.
So, in $\vartriangle DEC$,
$\tan \alpha = \dfrac{{DC}}{{EC}}$
Now, substitute the above value $DC = H - h$.
$
   \Rightarrow \tan \alpha = \dfrac{{H - h}}{{EC}} \\
   \Rightarrow EC = \dfrac{{H - h}}{{\tan \alpha }} \\
 $
So, our first part is done.
Now, let us find the length of $AB$ in terms of $h$.
So, in $\vartriangle EBA$,
$\tan \alpha = \dfrac{{EA}}{{AB}}$
Now, substitute the value that $EA = h$.
$
   \Rightarrow \tan \alpha = \dfrac{h}{{AB}} \\
   \Rightarrow AB = \dfrac{h}{{\tan \beta }} \\
 $
As we have discussed above,
Let us equate the values of $EC$ and $AB$ as their lengths are equal.
$ \Rightarrow EC = AB$
$ \Rightarrow \dfrac{{H - h}}{{\tan \alpha }} = \dfrac{h}{{\tan \beta }}$
Simplify the above equation to get the value of $H$ in terms of \[h\].
\[
   \Rightarrow H - h = \dfrac{{h \times \tan \alpha }}{{\tan \beta }} \\
   \Rightarrow H = \dfrac{{h \times \tan \alpha }}{{\tan \beta }} + h \\
   \Rightarrow H = \dfrac{{h \times \tan \alpha + h\tan \beta }}{{\tan \beta }} \\
   \Rightarrow H = \dfrac{{h\left( {\tan \alpha + \tan \beta } \right)}}{{\tan \beta }} \\
 \]
We know that the reciprocal of $\tan \theta $ is $\cot \theta $. Using this in the above equation we get,
\[ \Rightarrow H = h\left( {1 + \tan \alpha \cot \beta } \right)\]
Hence, we proved that the height of the other building is \[h\left( {1 + \tan \alpha \cot \beta } \right)\] meters.

Note:Select one of the triangles from the diagram and that selection must be useful for the future. In this way correlate all the unknown terms to form the equations with unknown values of variables. When we solve the equations, we will get the solution.Students should know the formula of trigonometric ratios,reciprocal of trigonometric functions and identities for solving these types of questions.