Question

A well of diameter is dug deep. The earth taken out of it has been spread evenly all around it in the shape of a circular ring of width to form an embankment. Find the height of the embankment.

Answer 1

Hint- For solving such questions draw a rough diagram for better understanding. Find out the total volume of earth dug first of all in order to find the volume of embankment and finally height of the embankment.

The shape of the well be cylindrical as shown in the given figure drawn

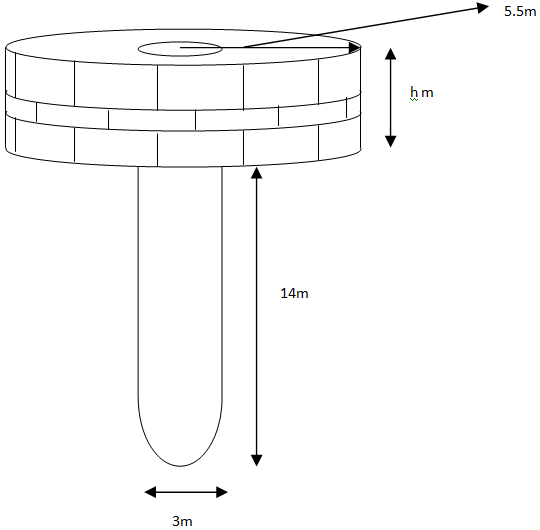
Given depth ${h_1}$ of the well $ = 14m$
Radius $\left( {{r_1}} \right)$ of the circular end of the well $ = \dfrac{3}{2}m$
Width of the embankment $ = 4m$
As show in the figure the embankment will also be in shape of hollow cylinder so, its outer radius is
$\left( {{r_2}} \right) = 4 + \dfrac{3}{2} = \dfrac{{11}}{2}m$
Let the height of the embankment be ${h_2}$.
So the volume of the soil dug from the well
= volume of the earth used to form the embankment
As, Volume of the soil dug
= volume of the cylinder
\[
   = \pi r_1^2{h_1} \\
   = \pi \times {\left( {\dfrac{3}{2}} \right)^2} \times 14 \\
   = \pi \times \dfrac{9}{4} \times 14 \\
 \] ---- (1)
Also volume of the embankment
=volume of hollow cylinder
\[
   = \pi \times \left( {r_2^2 - r_1^2} \right) \times {h_2} \\
   = \pi \times \left( {{{\left( {\dfrac{{11}}{2}} \right)}^2} - {{\left( {\dfrac{3}{2}} \right)}^2}} \right) \times {h_2} \\
   = \pi \times \left( {\left( {\dfrac{{121}}{4}} \right) - \left( {\dfrac{9}{4}} \right)} \right) \times {h_2} \\
   = \pi \times \left( {\dfrac{{112}}{4}} \right) \times {h_2} \\
 \] --- (2)
From equation (1) and (2), comparing to find the value of ${h_2}$.
$
   \Rightarrow \pi \times \left( {\dfrac{9}{4}} \right) \times 14 = \pi \times \left( {\dfrac{{112}}{4}} \right) \times {h_2} \\
   \Rightarrow \left( {\dfrac{9}{4}} \right) \times 14 = \left( {\dfrac{{112}}{4}} \right) \times {h_2} \\
   \Rightarrow {h_2} = \dfrac{9}{4} \times 14 \times \dfrac{4}{{112}} \\
   \Rightarrow {h_2} = \dfrac{9}{8} \\
   \Rightarrow {h_2} = 1.125m \\
$
Hence the height of the embankment will be $1.125m$.

Note- Figures are the most important part of questions containing these types of practical problems. Formulas of volume of cylinder, hollow cylinder and others are very useful and must be remembered. In order to solve problems of real life or practical type, try to relate it with some geometrical figures in order to solve the problem easily and fast.