Question

A water tank stands on the roof of a building as shown. Then the value of $ h $ (in $ m $ ) for which the distance covered by the water $ 'x' $ is greatest is

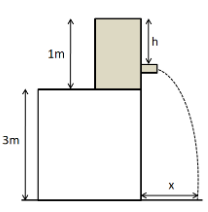
Answer 1

Hint: To solve this question, we need to use the Bernoulli’s theorem to get the horizontal velocity of water at the point from where it falls. Then, using the second kinematic equation of motion, we can determine the time of flight of water. Finally, multiplying the time of flight with the horizontal velocity will give us the expression for $ x $ which can be maximised to get the final answer.

Formula used: The formula used for solving this question is given by
 $ s = ut + \dfrac{1}{2}a{t^2} $ , here $ s $ is the displacement covered by a particle in $ t $ time with an initial velocity of $ u $ and an acceleration of $ a $ .

Complete step-by-step solution
We label two points A and B in the given figure as shown below.

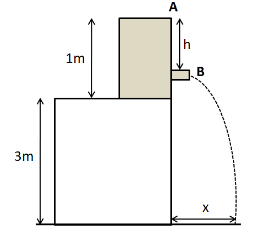
Now, we apply the Bernoulli’s theorem at points A and B to get
 $ {P_A} + \rho g{h_A} + \dfrac{1}{2}\rho v_A^2 = {P_B} + \rho g{h_B} + \dfrac{1}{2}\rho v_B^2 $
Now, the velocity of the water particles at point A will be zero. Also, the point A is at the top. So the pressure must be equal to the atmospheric pressure, $ {P_0} $ . Substituting $ {v_A} = 0 $ and $ {P_A} = {P_0} $ in the above equation we get
 $ {P_0} + \rho g{h_A} = {P_0} + \rho g{h_B} + \dfrac{1}{2}\rho v_B^2 $
 $ \Rightarrow \dfrac{1}{2}\rho v_B^2 = \rho g\left( {{h_B} - {h_A}} \right) $
From the above figure, we have $ {h_B} - {h_A} = h $ . So we get
 $ \dfrac{1}{2}\rho v_B^2 = \rho gh $
Cancelling $ \rho $ from both the sides, we get
 $ \dfrac{1}{2}v_B^2 = gh $
 $ \Rightarrow {v_B} = \sqrt {2gh} $ ...................(1)
This is the initial horizontal velocity of the water with which the water falls. But the initial vertical velocity of the water will be equal to zero. From the above figure, the vertical displacement covered by the water as it falls on the ground is
 $ y = \left( {4 - h} \right)m $
Now, from the second kinematic equation of motion we have
 $ y = ut + \dfrac{1}{2}a{t^2} $
Substituting $ u = 0 $ , $ y = \left( {4 - h} \right)m $ and $ a = g $ in the above equation, we get
 $ 4 - h = \dfrac{1}{2}g{t^2} $
 $ \Rightarrow t = \sqrt {2g\left( {4 - h} \right)} $ ...................(2)
Now, since the only force which acts on the water as it falls down is the gravitational force, which acts in the vertically downward direction, so the horizontal velocity of the water will remain constant. So the horizontal range covered by the water is given by
 $ x = {v_B}t $
Putting (1) and (2) in the above equation, we get
 $ x = \sqrt {2gh} \times \sqrt {2g\left( {4 - h} \right)} $
 $ \Rightarrow x = 2g\sqrt {h\left( {4 - h} \right)} $
Now, $ x $ will be greatest when the expression inside the square root is maximum. So we have to maximise this expression, which is given by
 $ f\left( h \right) = h\left( {4 - h} \right) $ ...................(3)
For maximising $ f\left( h \right) $ , we put
 $ f'\left( h \right) = 0 $
 $ \Rightarrow 4 - h - h = 0 $
On solving the above equation, we get
 $ h = 2m $
Hence, the distance covered by water is maximum when $ h $ is equal to $ 2m $ .

Note
Make sure to calculate the height covered by the water from the ground, before substituting it in the second equation of motion. Also, there is no need to maximize the expression of $ x $ in terms of $ h $ for maximizing it, as differentiating it will make it complex.