Question

A vessel is in the form of a hemispherical bowl surmounted by a hollow cylinder of the same diameter. The diameter of the hemispherical bowl is 14cm and the total height of the vessel is 13 cm. Find the total surface area of the vessel. $\left[ {{\text{Use }}\pi {\text{ = }}\dfrac{{22}}{7}} \right]$

Answer 1

Hint: Curved surface area of the cylinder is $2\pi rh$, and the Curved surface area of hemispherical bowl is $2\pi {r^2}$ use these formulas to reach the answer.

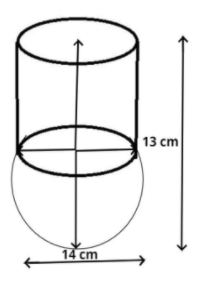
It is given that the diameter of the hemispherical bowl is equal to the diameter of the hollow cylinder which is 14 cm.
So the radius of the hemispherical bowl is also equal to the radius of hollow cylinder $ = \dfrac{{{\text{Diameter}}}}{2} = \dfrac{{14}}{2} = 7cm$
So, the height $\left( h \right)$ of the cylindrical portion = total height – radius of bowl
Total height of the vessel is 13 cm. (given)
$ \Rightarrow \left( h \right) = 13 - 7 = 6cm$
Now we know that the curved surface area of cylinder ${S_c} = 2\pi rh$
$ \Rightarrow {S_c} = 2 \times \dfrac{{22}}{7} \times 7 \times 6 = 264c{m^2}$
And we also know that the curved surface area of hemispherical portion ${S_b} = 2\pi {r^2} = 2 \times \dfrac{{22}}{7} \times {7^2} = 308c{m^2}$
So, the total surface area of the vessel is ${S_v} = {S_c} + {S_b}$
$ \Rightarrow {S_v} = 308 + 264 = 572c{m^2}$
So, this is the required surface area of the vessel.

Note: In such types of questions always remember the formula of curved surface area of cylinder and hemispherical bowl, then substitute the given values in these formulas and calculate the value of surface areas then add these surface areas to get the total surface area of the vessel, which is the required answer.