Question

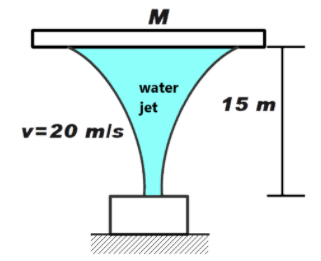
A vertical jet of water coming out of a nozzle with velocity 20 m/s supports a plate of mass M stationary at a height h = 15m, as shown in the figure if the rate of water flow is 1 litre per second the mass of the plate is (Assume the collision to be inelastic)
                        

A. 1 kg
B. 1.414 kg
C. 2 kg
D. 10 kg

Answer 1

Hint: In this question we have been asked to calculate the mass of the plate that is supported by a jet of water coming out of a nozzle with velocity 20 m/s, at a height of 15 m. we know that the mass of the plate will be equal to the force exerted by the jet of water on the plate. Therefore, we shall calculate the force exerted by the jet of water at height 15 m above the nozzle.

Complete answer:
We know that the plate is kept stationary at height 15 m by the water jet. Therefore, the weight of the plate will be equal to the force applied by the water jet.
Therefore, we can say that,
\[{{F}_{w}}=Mg\]………………… (1)
Now, for \[{{F}_{w}}\]
It is given that the rate of discharge is 1 litre per second.
We know that
\[1l/s={{10}^{-3}}{{m}^{3}}/s\]
We can say that the rate of discharge of water jet is the product of final velocity of water into the area.
Therefore,
\[AV={{10}^{-3}}{{m}^{3}}/s\] ……………. (2)
It is given that water leaves the nozzle at initial velocity u = 20 m/s. therefore applying energy conservation for the system to calculate final velocity V
We get,
\[\dfrac{1}{2}\rho {{u}^{2}}=\dfrac{1}{2}\rho {{V}^{2}}+\rho gh\]
Solving for V
\[{{V}^{2}}={{u}^{2}}-2gh\]
After substituting the values
We get,
\[{{V}^{2}}={{20}^{2}}-2\times 10\times 15\]
Therefore,
\[V=10m/s\]………………. (3)
The force exerted by the jet of water can be given by,
\[{{F}_{w}}=\rho A{{V}^{2}}\] …………… (4)
Now, from (1), (2), (3) and (4)
We get,
\[\rho A{{V}^{2}}=Mg\]
After substituting calculated values
We get,
\[{{10}^{3}}\times {{10}^{-3}}\times 10=M\times 10\]
Therefore,
\[M=1kg\]

Therefore, the correct answer is option A.

Note:
The law of conservation of energy states that energy can neither be created nor it can be destroyed. The energy can only be transformed from one form to another. Therefore, unless an external energy is added to the system due to force the energy of the system is conserved. Energy conservation helps us to calculate the important information about an object. If the mass and height of the object is known the potential energy of the object can be calculated using this concept.