Question

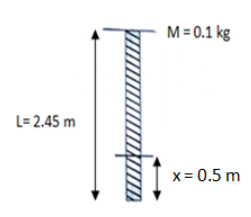
A uniform rope of mass $0.1\,kg$ and length $2.45\,m$ hangs from a ceiling
 $\left. i \right)$ The speed of the transverse wave in the rope at a point $0.5\,\,m$ distant from the lower end $\left. {ii} \right)$ the time taken by a transverse wave to travel the full length of rope is
$\left( {g = 9.8\,m/{s^2}} \right)$

A. $2.21\,m/s,\,\,1\,s$
B. $4.22\,m/s,\,\,2\,s$
C. $8.44\,m/s,\,\,4\,s$
D. $12\,m/s,\,\,6\,s$

Answer 1

Hint: Speed of a wave in a string is directly proportional to tension in the string and inversely proportional to mass per unit length. The tension created in a string is basically its own weight. The tension is not constant along the length of string because as we move upwards the mass of string hanging below increases, so tension increases therefore velocity increases.

Formula used:
$v = \sqrt {\dfrac{T}{\mu }} $

Complete answer:
 $\left. i \right)$ To calculate speed, firstly we need to calculate mass per unit length which is total mass divided by total length. $\mu = \dfrac{{0.1}}{{2.45}} = 0.04\,\,kg/m$
Also tension at a point $0.5\,\,m$ distant from the lower end is the weight of rope of $0.5\,\,m$.
$
  T = \mu \times 0.5 \times g \\
  T = 0.04 \times 0.5 \times 9.8 = 0.196\,\,\;N \\
 $
Then speed of wave $v = \sqrt {\dfrac{{0.196}}{{0.04}}} = 2.21\,\,m/s$
$\left. {ii} \right)$ As the tension at every point on the rope is different, the velocity of the wave at every point would also be different. Velocity is changing everywhere so we would need to calculate acceleration.
Velocity at any distance $x$ from lower end
$v = \sqrt {\dfrac{{\mu xg}}{\mu }} = \sqrt {xg} $
So acceleration of wave
 $
  \dfrac{{dv}}{{dt}} = \dfrac{{d\left( {\sqrt {xg} } \right)}}{{dt}} \\
  \dfrac{{dv}}{{dt}} = \dfrac{g}{2} \\
 $
Now the initial speed of the wave is zero because below the lower end no mass is present so tension is zero, therefore velocity is also zero.
The acceleration of the wave is constant so we can apply a second equation of motion to find time taken by the wave to travel the complete length of rope.
$
  2.42 = \dfrac{1}{2} \times \dfrac{g}{2} \times {t^2} \\
  \dfrac{{9.8}}{{9.8}} = {t^2} \\
  t = 1\,s \\
 $
So time taken by wave to travel the complete length of rope is $1\,s$.

So the correct option is $\left. A \right)$

Note:
The velocity of the wave increases as we move towards the upper end, because tension increases along the length, therefore do not get confused with the fact that acceleration is there in upward direction without any upward force.