Question

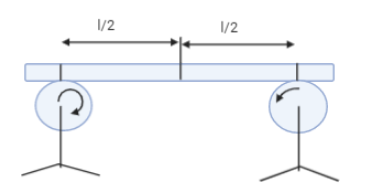
A uniform rod is placed on two spinning wheels as shown in the figure. The axes of the wheels are separated by l. The coefficient of friction between the rod and the wheel is $\mu $ . Show that the rod performs SHM and find the period of small oscillations.

A. $2\pi \sqrt {\dfrac{l}{{8g\mu }}} $
B. $2\pi \sqrt {\dfrac{l}{{4g\mu }}} $
C. $2\pi \sqrt {\dfrac{l}{{g\mu }}} $
D. $2\pi \sqrt {\dfrac{l}{{2g\mu }}} $

Answer 1

Hint:The total normal reaction force is equal to the weight of rod, the net frictional force is equal to the force due to acceleration of the rod and the torque produced due to the first spinning wheel is equal to the torque due to the second spinning wheel. The time period is calculated from these equations.

Complete step by step answer:
A uniform rod is kept on two spinning wheels (one is rotating clockwise and another is rotating anticlockwise) and the axes of the two wheels are separated by length l. When the forces acting between rod and two spinning wheels are balanced i.e., in equilibrium, the centre of mass lies at the midpoint of the rod. Now, let us move the rod by a distance x in a horizontal direction. So, the centre of mass also gets displaced by the same distance x from its balanced position. In equilibrium position, normal reaction forces and weight due to the rod is balanced i.e., ${N_1} + {N_2} = mg$ where m is the mass of the rod. Let it be equation 1.
The motion of the rod is due to the net frictional force acting between the rod and spinning wheels i.e.,$\mu {N_1} - \mu {N_2} = ma$ [a is acceleration of the rod, frictional force = $\mu N$ and N is normal reaction force]. Let it be equation 2.

In an axis perpendicular to the plane, the torque is zero i.e., the product of {N_1} and distance of the first spinning wheel from the new centre of mass is balanced to the product of {N_2} and distance of the second spinning wheel from the new centre of mass. Hence,
${N_1}\left( {\dfrac{l}{2} + x} \right) = {N_2}\left( {\dfrac{l}{2} - x} \right)$
$\Rightarrow {N_1}\left( {l + 2x} \right) = {N_2}\left( {l - 2x} \right)$
$\Rightarrow {N_2} = \dfrac{{{N_1}\left( {l + 2x} \right)}}{{l - 2x}}$ [equation 3]
Multiplying μ to the first equation, we get $\mu {N_1} + \mu {N_2} = \mu mg$ [equation 4]

Now, we add equation 2 and 4,$2\mu {N_1} = m\left( {a + \mu g} \right)$ [equation 5]
We put the value of {N_2} from equation 3 in equation 1,
${N_1} + \dfrac{{{N_1}\left( {l + 2x} \right)}}{{l - 2x}} = mg$
$\Rightarrow {N_1}\left( {l - 2x} \right) + {N_1}\left( {l + 2x} \right) = mg\left( {l - 2x} \right)$
$\Rightarrow {N_1}\left( {l - 2x + l + 2x} \right) = mg\left( {l - 2x} \right)$
$\Rightarrow 2l{N_1} = mg\left( {l - 2x} \right)$ [equation 6]

Now, we’ll divide equation 5 and 6,
$\dfrac{{2\mu {N_1}}}{{2l{N_1}}} = \dfrac{{m\left( {a + \mu g} \right)}}{{mg\left( {l - 2x} \right)}}$
$\Rightarrow\dfrac{\mu }{l} = \dfrac{{a + \mu g}}{{gl - 2gx}}$
$\Rightarrow\mu \left( {gl - 2gx} \right) = l\left( {a + \mu g} \right)$
$\Rightarrow \mu gl - 2\mu gx = la + l\mu g$
$\Rightarrow la = - 2\mu gx$
$\Rightarrow a = - \dfrac{{2\mu gx}}{l}$
$\Rightarrow a = \left| {\dfrac{{ - 2\mu gx}}{l}} \right|i.e.,\dfrac{{2\mu gx}}{l}$
Since, a is directly proportional to x as $\dfrac{{2\mu g}}{l}$ is constant and it is a simple harmonic motion because acceleration is directly proportional to the distance x in a SHM.
The time period of oscillations $\left( T \right) = 2\pi \sqrt {\dfrac{x}{a}} $
$T = 2\pi \sqrt {\dfrac{x}{{\dfrac{{2\mu gx}}{l}}}} $
$\therefore T = 2\pi \sqrt {\dfrac{l}{{2\mu g}}} $

Therefore, option D is correct.

Note: In an equilibrium, the total normal reaction force is equal to the weight of the rod and when the rod is displaced to a certain distance, the torque due to the first spinning wheel is equal to the torque due to the second spinning wheel.Most of the students don’t consider this and thus commit various mistakes.