Question

A uniform ladder of length L rests against the frictionless wall. The floor is rough and the coefficient of static friction between the floor and ladder is μ. When the ladder is positioned at angle θ, as shown in the accompanying, it is just about to slip. What is θ?

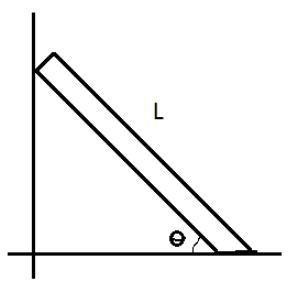
(A) \[\tan \theta =2\mu \]
(B) \[\cos \theta =\mu \]
(C) \[\tan \theta =\dfrac{1}{2\mu }\]
(D) \[\sin \theta =\dfrac{1}{\mu }\]

Answer 1

Hint:First all we have to make a free body diagram depicting clearly all the forces acting. Then we have to see whether any forces balance out each other or not. We have to then add the forces and arrive at our answer.

Complete step by step answer:

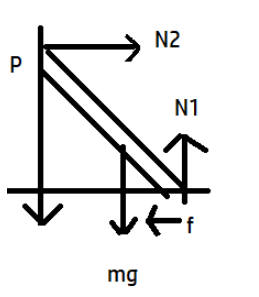
We have drawn a free body diagram and now we can easily solve this problem.
Since the body is in equilibrium, so sum of all the forces must be zero
In horizontal direction:
\[\begin{align}
&\Rightarrow {{N}_{2}}=f \\
&\Rightarrow {{N}_{2}}=\mu mg \\
\end{align}\]
where f is the frictional force due to the floor whose coefficient of friction is \[\mu \]
In vertical direction:
\[\Rightarrow {{N}_{1}}=mg\]
Since the body is inclined it has the tendency to rotate but there is no rotation so the sum of all torque acting on the body is zero.
\[\begin{align}
&\Rightarrow \sum{\tau }=0 \\
&\Rightarrow \dfrac{mgL\cos \theta }{2}+fL\sin \theta ={{N}_{1}}L\cos \theta \\
&\Rightarrow \dfrac{mgL\cos \theta }{2}+\mu mgL\sin \theta =mgL\cos \theta \\
&\Rightarrow \mu mgL\sin \theta =\dfrac{mgL\cos \theta }{2} \\
&\therefore \tan \theta =\dfrac{1}{2\mu } \\
\end{align}\]

So, the correct option comes out to be (C).

Note:Always keep in mind that frictional force opposes the relative motion of the two bodies. Here the ladder has the tendency to move leftwards, so frictional force acts towards right. Also, in accordance with Newton’s third law forces occur in pairs, that is the cause of origin of normal reaction.